
 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
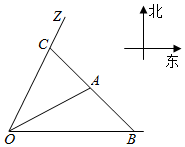 为了寻找马航MH370残骸,我国“雪龙号”科考船于2014年3月26日从港口O出发,沿北偏东15°角的射线OZ方向航行,而在港口北偏东60°角的方向上有一个给科考船补给物资的小岛A,OA=100(1+$\sqrt{3}$)海里,现指挥部需要紧急征调位于港口O正东x(x>200)海里的B处的补给船,速往小岛A装上补给物资供给科考船,该船沿BA方向全速追赶科考船,并在C相遇,经测算当两船运行的航线与海岸线OB围成的三角形OBC的面积S小时,这种补给方案最优.
为了寻找马航MH370残骸,我国“雪龙号”科考船于2014年3月26日从港口O出发,沿北偏东15°角的射线OZ方向航行,而在港口北偏东60°角的方向上有一个给科考船补给物资的小岛A,OA=100(1+$\sqrt{3}$)海里,现指挥部需要紧急征调位于港口O正东x(x>200)海里的B处的补给船,速往小岛A装上补给物资供给科考船,该船沿BA方向全速追赶科考船,并在C相遇,经测算当两船运行的航线与海岸线OB围成的三角形OBC的面积S小时,这种补给方案最优.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com