
分析 (1)由椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{25}$=1,可得焦点G,不妨取G(0,4),把y=4代入抛物线方程可得:42=2px,解得xH=$\frac{8}{p}$.由于|HF|=2|GH|,可得$\frac{8}{p}$+$\frac{p}{2}$=2×$\frac{8}{p}$,解得p即可得出.
(2)设A(x1,y1),B(x2,y2),则点P$(\frac{{x}_{1}+{x}_{2}}{2},\frac{{y}_{1}+{y}_{2}}{2})$,由题意可设直线l1d的方程为:y=k(x-2)(k≠0).与抛物线方程联立化为k2x2-(4k2+8)x+4k2=0,△>0,利用根与系数的关系、中点坐标公式可得点P$(2+\frac{4}{{k}^{2}},\frac{4}{k})$.由题意可知:直线l2的斜率为-$\frac{1}{k}$,同理可得Q(2+4k2,-4k).k≠±1时,直线PQ的斜率kPQ=$\frac{\frac{4}{k}+4k}{\frac{4}{{k}^{2}}-4{k}^{2}}$=$\frac{k}{1-{k}^{2}}$,直线PQ的方程为:k(x-6)-(1-k2)y=0,于是直线PQ恒过定点E(6,0),k=±1时,直线PQ也经过点E(6,0).
(3)由点P$(2+\frac{4}{{k}^{2}},\frac{4}{k})$,Q(2+4k2,-4k).可得:|PQ|2=$\frac{16}{{k}^{4}}+16{k}^{4}-32+\frac{16}{{k}^{2}}+16{k}^{2}+32$≥64.当且仅当k=±1时取等号,此时△FPQ为直角三角形,△FPQ外接圆面积S=$π(\frac{|PQ|}{2})^{2}$,即可得出最小值.
解答  解:(1)由椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{25}$=1,可得焦点G(0,±4),
解:(1)由椭圆$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{25}$=1,可得焦点G(0,±4),
不妨取G(0,4),把y=4代入抛物线方程可得:42=2px,解得xH=$\frac{8}{p}$.
∵|HF|=2|GH|,∴$\frac{8}{p}$+$\frac{p}{2}$=2×$\frac{8}{p}$,p>0,解得p=4.
∴抛物线C的方程为y2=8x.
(2)设A(x1,y1),B(x2,y2),则点P$(\frac{{x}_{1}+{x}_{2}}{2},\frac{{y}_{1}+{y}_{2}}{2})$,
由题意可设直线l1d的方程为:y=k(x-2)(k≠0).
由$\left\{\begin{array}{l}{{y}^{2}=8x}\\{y=k(x-2)}\end{array}\right.$,化为k2x2-(4k2+8)x+4k2=0,△=64k2+64>0,
∵直线l1交C于两点A,B,∴x1+x2=4+$\frac{8}{{k}^{2}}$,y1+y2=k(x1+x2-4)=$\frac{8}{k}$,可得点P$(2+\frac{4}{{k}^{2}},\frac{4}{k})$.
由题意可知:直线l2的斜率为-$\frac{1}{k}$,同理可得Q(2+4k2,-4k).
k≠±1时,有$2+\frac{4}{{k}^{2}}$≠2+4k2.直线PQ的斜率kPQ=$\frac{\frac{4}{k}+4k}{\frac{4}{{k}^{2}}-4{k}^{2}}$=$\frac{k}{1-{k}^{2}}$,
直线PQ的方程为:y+4k=$\frac{k}{1-{k}^{2}}$(x-2-4k2),整理为k(x-6)-(1-k2)y=0,于是直线PQ恒过定点E(6,0),
k=±1时,直线PQ的方程为:x=6,也经过点E(6,0).
综上所述:直线PQ恒过定点E(6,0).
(3)由点P$(2+\frac{4}{{k}^{2}},\frac{4}{k})$,Q(2+4k2,-4k).
可得:|PQ|2=$[2+\frac{4}{{k}^{2}}-(2+4{k}^{2})]^{2}$+$(\frac{4}{k}+4k)^{2}$=$\frac{16}{{k}^{4}}+16{k}^{4}-32+\frac{16}{{k}^{2}}+16{k}^{2}+32$$≥2\sqrt{1{6}^{2}}+2\sqrt{1{6}^{2}}$=64.
当且仅当k=±1时取等号,此时△FPQ为直角三角形,
△FPQ外接圆面积S=$π(\frac{|PQ|}{2})^{2}$=$\frac{π}{4}|PQ{|}^{2}$,
故当|PQ|2取最小值64时,S取得最小值16π.
点评 本题考查了椭圆与抛物线的标准方程及其性质、斜率计算公式、直线与抛物线相交问题、三角形面积计算公式、基本不等式的性质、一元二次方程的根与系数的关系,考查了推理能力与计算能力,属于难题.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
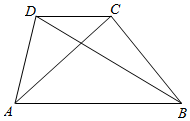 如图,在梯形ABCD中,AB∥CD,AD=6,cos∠ADC=-$\frac{1}{3}$.
如图,在梯形ABCD中,AB∥CD,AD=6,cos∠ADC=-$\frac{1}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
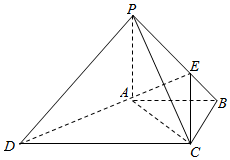
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| k | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | >7 |
| p | 0.03 | 0.10 | 0.14 | 0.19 | 0.21 | 0.19 | 0.09 | 0.04 | 0.01 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com