
分析 分别求出两函数的导数,可得切线的斜率,再由两直线垂直的条件:斜率之积为-1,运用参数分离和换元法,结合对勾函数的单调性,即可得到所求范围.
解答 解:y=(ax-1)ex的导数为y′=(ax-1+a)ex,
可得切线l1的斜率为(ax0-1+a)ex0,
y=(1-x)e-x的导数为y′=(x-2)e-x,
可得切线l2的斜率为(x0-2)e-x0,
由l1⊥l2,可得(ax0-1+a)ex0•(x0-2)e-x0=-1,
即为a=$\frac{3-{x}_{0}}{(2-{x}_{0})(1+{x}_{0})}$,0<x0<1,
令3-x0=t(2<t<3),即x0=3-t,
可得a=$\frac{t}{(4-t)(t-1)}$=$\frac{1}{5-(t+\frac{4}{t})}$,
由t+$\frac{4}{t}$在(2,3)递增,可得t+$\frac{4}{t}$∈(4,$\frac{13}{3}$),
即有$\frac{1}{5-(t+\frac{4}{t})}$∈(1,$\frac{3}{2}$).
则则实数a的取值范围是(1,$\frac{3}{2}$).
故答案为:(1,$\frac{3}{2}$).
点评 本题考查导数的运用:求切线的斜率,考查两直线垂直的条件:斜率之积为-1,同时考查换元法和对勾函数的单调性的运用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{3\sqrt{2}}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
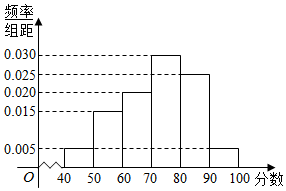 某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.
某校从参加高二年级学业水平测试的学生中抽出80名学生,其数学成绩(均为整数)的频率分布直方图如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com