
在等差数列 中,已知
中,已知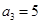 ,
,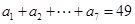 .
.
(1)求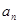 ;
;
(2)若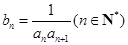 ,设数列
,设数列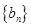 的前
的前 项和为
项和为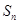 ,试比较
,试比较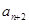 与
与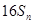 的大小.
的大小.
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:解答题
水土流失是我国西部大开发中最突出的问题,全国9100万亩坡度为25°以上的坡耕地需退耕还林,其中西部占70%,2002年国家确定在西部地区退耕还林面积为515万亩,以后每年退耕土地面积递增12%.
(1)试问,从2002年起到哪一年西部地区基本上解决退耕还林问题?
(2)为支持退耕还林工作,国家财政补助农民每亩300斤粮食,每斤粮食按0.7元计算,并且每亩退耕地每年补助20元,试问到西部地区基本解决退耕还林问题时,国家财政共需支付约多少亿元?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在等差数列{an}中,a2+a7=-23,a3+a8=-29.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设数列{an+bn}是首项为1,公比为c的等比数列,求数列{bn}的前n项和Sn.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知数列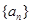 的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.数列
的奇数项是首项为1的等差数列,偶数项是首项为2的等比数列.数列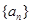 前
前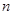 项和为
项和为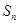 ,且满足
,且满足
(1)求数列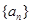 的通项公式;
的通项公式;
(2)求数列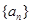 前
前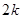 项和
项和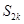 ;
;
(3)在数列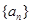 中,是否存在连续的三项
中,是否存在连续的三项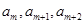 ,按原来的顺序成等差数列?若存在,求出所有满足条件的正整数
,按原来的顺序成等差数列?若存在,求出所有满足条件的正整数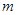 的值;若不存在,说明理由.
的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com