
【题目】如图所示的空间几何体![]() 中,四边形
中,四边形![]() 是边长为2的正方形,
是边长为2的正方形, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
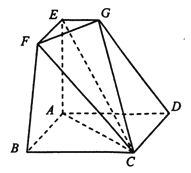
(1)求证:平面![]() 平面
平面![]() ;
;
(2)求平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值.
所成的锐二面角的余弦值.
【答案】(Ⅰ)详见解析(Ⅱ)![]()
【解析】试题分析:(I)连接![]() 交
交![]() 于点
于点![]() ,根据正方形的对角线有
,根据正方形的对角线有![]()
![]() ,设
,设![]() 的中点分别为
的中点分别为![]() ,连接
,连接![]() ,得
,得![]() ,连接
,连接![]() ,利用平行证得
,利用平行证得![]() ,而
,而![]() ,所以
,所以![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .(2)以
.(2)以![]() 为坐标原点建立空间直角坐标系,计算平面
为坐标原点建立空间直角坐标系,计算平面![]() 与平面
与平面![]() 的法向量,并由此计算二面角的余弦值.
的法向量,并由此计算二面角的余弦值.
试题解析:
(1)证明:连接![]() 交
交![]() 于点
于点![]() ,则
,则![]()
![]()
设![]() ,
, ![]() 的中点分别为
的中点分别为![]() ,
, ![]() ,连接
,连接![]() ,则
,则![]() ∥
∥![]() ,
,
连接![]() ,
, ![]() ,则
,则![]() ∥
∥![]() 且
且![]()
![]() ,所以
,所以![]() ∥
∥![]() ,所以
,所以![]() ∥
∥![]()
由于![]() 平面
平面![]() ,所以
,所以 ![]()
![]()
所以![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]()
所以平面![]() 平面
平面![]()
(2)解法一:∵![]() ∥
∥![]() ,∴
,∴![]() ∥
∥![]()
∴平面![]() 与平面
与平面![]() 所成的锐二面角即为平面
所成的锐二面角即为平面![]() 与平面
与平面![]() 所成的锐二面角
所成的锐二面角
连接![]() ,∵
,∵![]() 平面
平面![]() ,
, ![]() ∴
∴![]()
![]()
∴![]() 为平面
为平面![]() 与平面
与平面![]() 所成二面角的一个平面角
所成二面角的一个平面角
∵![]() ,
, ![]() ∴
∴![]()
∴![]()
即平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为![]()
解法二:建立如图所示空间直角坐标系![]() ,
,

则![]() ,
, ![]()
依题意![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
设![]() 为平面
为平面![]() 的一个法向量,则
的一个法向量,则
 即
即![]() 令
令![]() ,
,
则![]() ,所以
,所以![]()
设平面![]() 与平面
与平面![]() 所成的锐二面角为
所成的锐二面角为![]() ,则
,则
即平面![]() 与平面
与平面![]() 所成的锐二面角的余弦值为
所成的锐二面角的余弦值为![]()


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以直角坐标系的原点O为极点, ![]() 轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知过点P(1,1)的直线
轴的正半轴为极轴,且两个坐标系取相等的单位长度.已知过点P(1,1)的直线![]() 的参数方程是
的参数方程是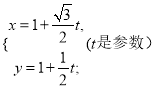
(I)写出直线![]() 的极坐标方程;
的极坐标方程;
(II)设![]() 与圆
与圆![]() 相交于两点A、B,求点P到A、B两点的距离之积
相交于两点A、B,求点P到A、B两点的距离之积
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
有甲、乙、丙、丁四名网球运动员,通过对过去战绩的统计,在一场比赛中,甲对乙、丙、丁取胜的概率分别为![]() .
.
(Ⅰ)若甲和乙之间进行三场比赛,求甲恰好胜两场的概率;
(Ⅱ)若四名运动员每两人之间进行一场比赛,设甲获胜场次为![]() ,求随机变量
,求随机变量![]() 的分布列及期望
的分布列及期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]() “存在
“存在![]() ”,命题
”,命题![]() :“曲线
:“曲线![]() 表示焦点在
表示焦点在![]() 轴上的椭圆”,命题
轴上的椭圆”,命题![]() “曲线
“曲线![]() 表示双曲线”
表示双曲线”
(1)若“![]() 且
且![]() ”是真命题,求实数
”是真命题,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 是
是![]() 的必要不充分条件,求实数
的必要不充分条件,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,多面体![]() 中,四边形
中,四边形![]() 是菱形,
是菱形, ![]() ,
, ![]() 相交于
相交于![]() ,
, ![]() ,点
,点![]() 在平面
在平面![]() 上的射影恰好是线段
上的射影恰好是线段![]() 的中点.
的中点.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求平面
,求平面![]() 与平面
与平面![]() 所成角(锐角)的余弦值.
所成角(锐角)的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,
, ![]() 分别是它的左、右焦点,且存在直线
分别是它的左、右焦点,且存在直线![]() ,使
,使![]() 关于
关于![]() 的对称点恰好是圆
的对称点恰好是圆![]() (
(![]() )的一条直线的两个端点.
)的一条直线的两个端点.
(1)求椭圆![]() 的方程;
的方程;
(2)设直线![]() 与抛物线
与抛物线![]() (
(![]() )相交于
)相交于![]() 两点,射线
两点,射线![]() ,
, ![]() 与椭圆
与椭圆![]() 分别相交于点
分别相交于点![]() ,试探究:是否存在数集
,试探究:是否存在数集![]() ,当且仅当
,当且仅当![]() 时,总存在
时,总存在![]() ,使点
,使点![]() 在以线段
在以线段![]() 为直径的圆内?若存在,求出数集
为直径的圆内?若存在,求出数集![]() ;若不存在,请说明理由.
;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国际奥委会将于2017年9月15日在秘鲁利马召开130次会议决定2024年第33届奥运会举办地。目前德国汉堡、美国波士顿等申办城市因市民担心赛事费用超支而相继退出。某机构为调查我国公民对申办奥运会的态度,选了某小区的100位居民调查结果统计如下:

(1)根据已有数据,把表格数据填写完整;
(2)能否在犯错误的概率不超过5%的前提下认为不同年龄与支持申办奥运无关?
(3)已知在被调查的年龄大于50岁的支持者中有5名女性,其中2位是女教师,现从这5名女性中随机抽取3人,求至多有1位教师的概率.
附:  ,
, ![]() .
.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com