【题目】已知
是椭圆
上一点， 
为椭圆的两焦点，且
，则
面积为（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
由椭圆的标准方程可得：c＝4，设|PF1|＝t1，|PF2|＝t2，根据椭圆的定义可得：t1+t2＝10，再根据余弦定理可得：t12+t22﹣t1t2＝64，再联立两个方程求出t1t2＝12，进而结合三角形的面积公式求出三角形的面积．
由椭圆的标准方程可得：a＝5，b＝3，
∴c＝4，
设|PF1|＝t1，|PF2|＝t2，
所以根据椭圆的定义可得：t1+t2＝10①，
在△F1PF2中，∠F1PF2＝60°，
所以根据余弦定理可得：|PF1|2+|PF2|2﹣2|PF1||PF2|cos60°＝|F1F2|2＝（2c）2＝64，
整理可得：t12+t22﹣t1t2＝64，②
把①两边平方得t12+t22+2t1t2＝100，③
所以③﹣②得t1t2＝12，
∴
∠F1PF2＝3
．
故选A．
科目：高中数学 来源： 题型：
【题目】定义域为
的函数
满足：
，且对于任意实数
，
恒有
，当
时，
.
（1）求
的值，并证明当
时，
；
（2）判断函数在上的单调性并加以证明；
（3）若不等式
对任意
恒成立，求实数
的取值范围.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】求适合下列条件的双曲线的标准方程：
(1)过点(3，－
)，离心率e＝
；
(2)中心在原点，焦点F1，F2在坐标轴上，实轴长和虚轴长相等，且过点P(4，－
)．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在三棱柱
中，
，顶点
在底面
上的射影恰为点
，且
（1）证明：平面
平面
；
（2）求棱
与
所成的角的大小；
（3）若点
为
的中点，并求出二面角
的平面角的余弦值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设P是抛物线y2=4x上的一个动点，F为抛物线的焦点，记点P到点A（-1,1）的距离与点P到直线x= - 1的距离之和的最小值为M，若B（3,2），记|PB|+|PF|的最小值为N，则M+N= ______________
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，四边形ABCD是正方形，PA
平面ABCD，EB//PA,AB=PA=4，EB=2，F为PD的中点.
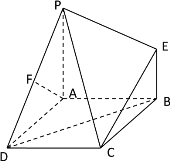
（1）求证AFPC
（2）BD//平面PEC
（3）求二面角D-PC-E的大小
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】下图是某省从1月21日至2月24日的新冠肺炎每日新增确诊病例变化曲线图.
若该省从1月21日至2月24日的新冠肺炎每日新增确诊人数按日期顺序排列构成数列
，的前n项和为
，则下列说法中正确的是（ ）
A.数列是递增数列B.数列
是递增数列
C.数列的最大项是
D.数列的最大项是
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
