
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 首先画出分段函数f(x)的图形,由题意知:f(f(x))=-1,可解得:f(x)=-2 或 f(x)=$\frac{1}{2}$;利用数形结合法可直接判断交点个数;
解答 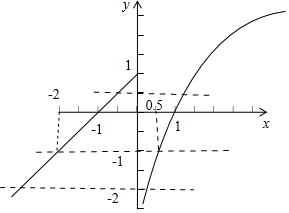 解:根据f(x)表达式画出f(x)图形如右图.
解:根据f(x)表达式画出f(x)图形如右图.
由题意知:f(f(x))=-1,可解得:f(x)=-2 或 f(x)=$\frac{1}{2}$;
当f(x)=-2时,f(x)图形与直线y=-2有两个交点;
当f(x)=$\frac{1}{2}$时,f(x)图形与直线y=$\frac{1}{2}$有两个交点;
综上,f(f(x))+1=0有4个解;
故选:D
点评 本题主要考查了分段函数的图形画法,以及方程根与图形交点的转换与数形结合思想的应用,属中等题.


科目:高中数学 来源: 题型:选择题
| A. | λ1=λ2=1 | B. | λ1=λ2=-1 | C. | λ1λ2=1 | D. | λ1λ2=-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
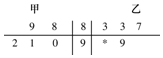 下面茎叶图表示的是甲、乙两人在5次综合测评中的成绩(成绩为整数,满分为100),其中一个数字被污损,则乙的平均成绩不低于甲的平均成绩的概率为( )
下面茎叶图表示的是甲、乙两人在5次综合测评中的成绩(成绩为整数,满分为100),其中一个数字被污损,则乙的平均成绩不低于甲的平均成绩的概率为( )| A. | $\frac{2}{5}$ | B. | $\frac{1}{10}$ | C. | $\frac{9}{10}$ | D. | $\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\{x|-2<x<\frac{1}{3}\}$ | B. | $\{x|x>\frac{1}{3}$或x<-2} | C. | $\{x|-\frac{1}{3}≤x≤2\}$ | D. | {x|x<-3或$x>\frac{1}{2}\}$ |
查看答案和解析>>
科目:高中数学 来源:2017届江西吉安一中高三上学期段考一数学(理)试卷(解析版) 题型:解答题
某电视台举行一个比赛类型的娱乐节目,  两队各有六名选手参赛,将他们首轮的比赛成绩作为样本数据,绘制成茎叶图如图所示,为了增加节目的趣味性,主持人故意将
两队各有六名选手参赛,将他们首轮的比赛成绩作为样本数据,绘制成茎叶图如图所示,为了增加节目的趣味性,主持人故意将 队第六位选手的成绩没有给出,并且告知大家
队第六位选手的成绩没有给出,并且告知大家 队的平均分比
队的平均分比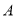 队的平均分多4分,同时规定如果某位选手的成绩不少于21分,则获得“晋级”.
队的平均分多4分,同时规定如果某位选手的成绩不少于21分,则获得“晋级”.

(1)根据茎叶图中的数据,求出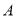 队第六位选手的成绩;
队第六位选手的成绩;
(2)主持人从 队所有选手成绩中随机抽2个,求至少有一个为“晋级”的概率;
队所有选手成绩中随机抽2个,求至少有一个为“晋级”的概率;
(3)主持人从 两队所有选手成绩分别随机抽取2个,记抽取到“晋级”选手的总人数为
两队所有选手成绩分别随机抽取2个,记抽取到“晋级”选手的总人数为 ,求
,求 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com