
分析 利用F($\sqrt{2}$,0)为其右焦点,过F垂直于x轴的直线与椭圆相交所得的弦长为2,建立方程组,求解即可得椭圆方程.
解答 解:∵椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0),F($\sqrt{2}$,0)为其右焦点,
过F垂直于x轴的直线与椭圆相交所得的弦长为2,
∴$\left\{\begin{array}{l}{c=\sqrt{2}}\\{\frac{2{b}^{2}}{a}=2}\\{{a}^{2}={b}^{2}+{c}^{2}}\end{array}\right.$,解得a2=4,b2=2,c2=2,
∴椭圆C的方程为:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{2}=1$.
故答案为:$\frac{x^2}{4}+\frac{y^2}{2}=1$.
点评 本题主要考查了直线与圆锥曲线的综合问题、椭圆的标准方程问题,常可利用联立方程进而求解的方法,是中档题.


科目:高中数学 来源: 题型:解答题

| 组号 | 分组 | 频数 | 频率 |
| 1 | [55,60) | 5 | 0.05 |
| 2 | [60,65) | 20 | 0.29 |
| 3 | [65,70) | ||
| 4 | [70,75) | 35 | 0.35 |
| 5 | [75,80) | ||
| 6 | [80,85) | ||
| 合计 | 100 | 1.00 | |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
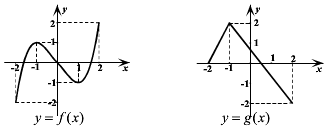
| A. | ②③④ | B. | ①④ | C. | ②③ | D. | ①②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0)∪(4,+∞) | B. | (-∞,2)∪(4,+∞) | C. | (2,4) | D. | (0,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2017届江西吉安一中高三上学期段考一数学(理)试卷(解析版) 题型:解答题
选修4-5:不等式选讲
已知适合不等式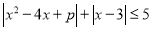 的
的 的最大值为3.
的最大值为3.
(1)求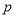 的值;
的值;
(2)求 的范围.
的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com