
分析 (1)利用赋值法结合条件进行转化求解证明即可.
(2)根据抽象函数的关系进行转化,结合函数单调性进行求解即可.
解答 解:(1)令x=0,y=0得f(0)=$\frac{f(0)}{f(0)}$=1,
∴f(0)=1…(1分)
令x=a+b,y=b,则x-y=a,
又∵f(x-y)=$\frac{f(x)}{f(y)}$,
∴f(a+b)=f(a)•f(b)…(4分)
∴f(x+y)=f(x)•f(y)…(5分),
(2)由(1)知f(x2)•f(10)=f(x2+10),
∴$\frac{{f({x^2})•f(10)}}{f(7x)}$=$\frac{f({x}^{2}+10)}{f(7x)}$=f(x2-7x+10),
又∵f(-1)=3,∴9=3×3=f(-1)×f(-1)=f(-2)…(8分)
又∵$\frac{{f({x^2})•f(10)}}{f(7x)}$≤9.
∴f(x2-7x+10)≤f(-2)…(9分)
又∵f(x)在R上单调递减,
∴x2-7x+10≥-2…(10分),
解得:x≤3或x≥4,即原不等式的解集为(-∞,3)∪(4,+∞)…(12分)
点评 本题主要考查抽象函数的应用,利用条件结合赋值法是解决本题的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
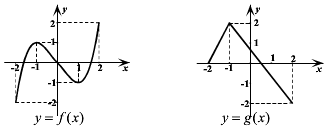
| A. | ②③④ | B. | ①④ | C. | ②③ | D. | ①②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,0)∪(4,+∞) | B. | (-∞,2)∪(4,+∞) | C. | (2,4) | D. | (0,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源:2017届江西吉安一中高三上学期段考一数学(文)试卷(解析版) 题型:解答题
选修4-5:不等式选讲
已知函数 .
.
(1)解不等式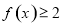 ;
;
(2)对任意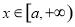 ,都有
,都有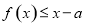 成立,求实数
成立,求实数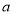 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com