
 的弦,端点A与A′、B与B′的横坐标分别相等,纵坐标分别同号.
的弦,端点A与A′、B与B′的横坐标分别相等,纵坐标分别同号. ,求椭圆C的方程;
,求椭圆C的方程; ,试探究弦A′B′是否也必过某个定点.
,试探究弦A′B′是否也必过某个定点.
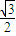 ,求出几何量,即可求得椭圆C的方程;
,求出几何量,即可求得椭圆C的方程;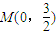 ,确定直线A′B′的方程,从而可得弦A′B′必过定点;
,确定直线A′B′的方程,从而可得弦A′B′必过定点; 倍可得到椭圆C,端点A与A′、B与B′的横坐标分别相等,纵坐标分别同号,由弦AB过定点
倍可得到椭圆C,端点A与A′、B与B′的横坐标分别相等,纵坐标分别同号,由弦AB过定点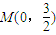 ,猜想弦A′B′过定点
,猜想弦A′B′过定点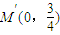 ,进一步可证得结论.
,进一步可证得结论.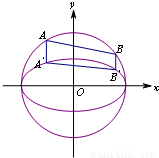 解:(Ⅰ)由题意得,b=1,
解:(Ⅰ)由题意得,b=1,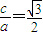 ,…(2分)
,…(2分)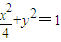 .…(4分)
.…(4分)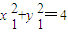 ,…①
,…①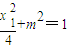 ,…②
,…②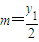 ,同理解得:
,同理解得: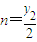 .
.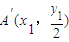 、
、 .…(8分)
.…(8分)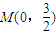 ,
,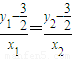 ,
,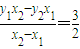 …(10分)
…(10分)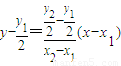 ,即
,即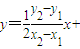
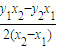 ,
,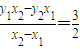 得直线A′B′的方程为:
得直线A′B′的方程为: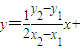
 ,
,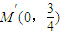 .…(12分)
.…(12分) 倍可得到椭圆C,
倍可得到椭圆C,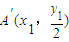 、
、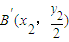 .…(8分)
.…(8分)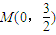 ,猜想弦A′B′过定点
,猜想弦A′B′过定点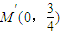 .…(9分)
.…(9分)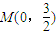 ,
,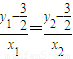 …①…(10分)
…①…(10分)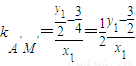 ,
,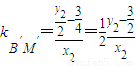 ,
,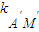 =
=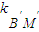 ,
,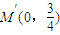 .…(12分)
.…(12分)

 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
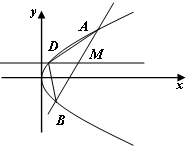
 (2012•泉州模拟)如图,设AB、A′B′分别是圆O:x2+y2=a2和椭圆C:
(2012•泉州模拟)如图,设AB、A′B′分别是圆O:x2+y2=a2和椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
| 3 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知抛物线C:y2=2px(p>0)上有一点Q(2,y0)到焦点F的距离为
已知抛物线C:y2=2px(p>0)上有一点Q(2,y0)到焦点F的距离为| 5 | 2 |
查看答案和解析>>
科目:高中数学 来源:2010年江苏省扬州中学高三第四次模拟考试数学试题 题型:解答题
[选做题]
A.选修4—1:几何证明选讲
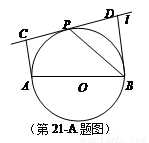
如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD,求证:
(1)l是⊙O的切线;
(2)PB平分∠ABD.
|
 对应的变换将点
对应的变换将点 与
与 分别变换成点
分别变换成点 与
与 .求矩阵
.求矩阵 ;
; 的最大值.
的最大值.查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省、金陵中学、南京外国语学校高三三校联考数学卷 题型:解答题
A.选修4-1:几何证明选讲
|
如图,设AB为⊙O的任一条不与直线l垂直的直径,P是⊙O与l的公共点,AC⊥l,BD⊥l,垂足分别为C,D,且PC=PD.求证:(1)l是⊙O的切线;(2)PB平分∠ABD.
B.选修4-2:矩阵与变换
(本小题满分10分)
已知点A在变换:T:→=作用后,再绕原点逆时针旋转90°,得到点B.若点B坐标为(-3,4),求点A的坐标.
C.选修4-4:坐标系与参数方程
(本小题满分10分)
求曲线C1:被直线l:y=x-所截得的线段长.
D.选修4-5:不等式选讲
(本小题满分10分)
已知a、b、c是正实数,求证:≥.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com