设函数f(x)=x|x|+bx+c(x∈R)给出下列4个命题:
①当b=0,c=0时,f(x)=0只有一个实数根;
②当c=0时,y=f(x)是偶函数;
③函数y=f(x)的图象关于点(0,c)对称;
④当b≠0,c≠0时,方程f(x)=0有两个实数根.
上述命题中,所有正确命题的个数是 .
【答案】
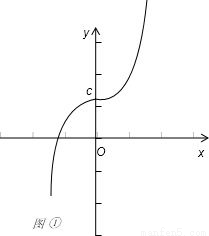
分析:根据题意,依次分析四个命题:①当b=0,c=0时,f(x)=x|x|=0只有一个实数根0; ②当c=0时,y=f(x)=x|x|+bx是奇函数;③设g(x)=x|x|+bx,因为g(-x)=-x|-x|+b(-x)=-g(x),所以g(x)=x|x|+bx关于(0,0)对称,又函数y=f(x)的图象可以由g(x)=x|x|+bx的图象上下平移c个单位得到.故函数y=f(x)的图象关于点(0,c)对称;④当c=0,b<0时,f(x)=x|x|+bx=
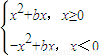
,方程f(x)=0可以有三个实数根.
解答:解:由f(x)=x|x|+bx+c(x∈R),知:
①当b=0,c=0时,f(x)=x|x|=0只有一个实数根0,故①正确;
②当c=0时,y=f(x)=x|x|+bx是奇函数,故②正确;
③设g(x)=x|x|+bx,因为g(-x)=-x|-x|+b(-x)=-g(x),所以g(x)=x|x|+bx关于(0,0)对称,又函数y=f(x)的图象可以由g(x)=x|x|+bx的图象上下平移c个单位得到.故函数y=f(x)的图象关于点(0,c)对称,故③正确;
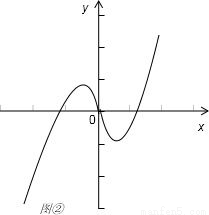
④当c=0,b<0时,如图②,f(x)=x|x|+bx=
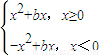
,方程f(x)=0可以有三个实数根.
故④不成立.
故答案为:3个.
点评:本题考查真假命题的判断、函数的奇偶性,方程根的个数判断,体现了数形结合的数学思想.

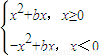 ,方程f(x)=0可以有三个实数根.
,方程f(x)=0可以有三个实数根.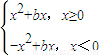 ,方程f(x)=0可以有三个实数根.
,方程f(x)=0可以有三个实数根.



 名校课堂系列答案
名校课堂系列答案