Question

2．在梯形ABCD中，AB=a，CD=b，a＜b，EF为一线段，若S_{四边形ABFE}=S_{四边形CDEF}，且∠BFE=∠D，求EF的长（用a，b表示）．

Answer 1

分析 根据相似三角形的性质得到比例式，求出EF的长即可．

解答 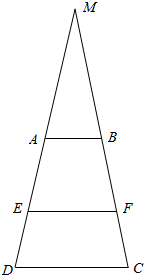解：如图示：延长DA、CB交于点M，设△MAB面积=s，
∵AB∥CD
∴∠MAB=∠ADC，又由∠M是公共角，
∴△MAB∽△MDC
∴$\frac{{S}_{△MAB}}{{S}_{△MDC}}$=$\frac{{AB}^{2}}{{CD}^{2}}$，即：$\frac{s}{{S}_{△MDC}}$=$\frac{{a}^{2}}{{b}^{2}}$，∴S_△MDC=$\frac{{sb}^{2}}{{a}^{2}}$，
∴S_梯形ABCD=S_△MDC-S_△MAB=$\frac{s{（b}^{2}{-a}^{2}）}{{a}^{2}}$，
∵四边形ABFE的面积与四边形CDEF的面积相等，
∴S_{四边形ABEF}=$\frac{1}{2}$S_梯形ABCD=$\frac{1}{2}$•$\frac{s{（b}^{2}{-a}^{2}）}{{a}^{2}}$，
∴S_△MEF=S_△MAB+S_{四边形ABEF}=s+$\frac{s{（b}^{2}{-a}^{2}）}{{2a}^{2}}$=$\frac{s{（b}^{2}{+a}^{2}）}{{2a}^{2}}$，
∵∠BFE=∠ADC
∴∠MAB=∠BFE，又∠M是公共角，
∴△MAB∽△MFE
∴$\frac{{S}_{△MAB}}{{S}_{△MEF}}$=$\frac{{AB}^{2}}{{EF}^{2}}$，即：$\frac{s}{\frac{s{（b}^{2}{+a}^{2}）}{{2a}^{2}}}$=$\frac{{a}^{2}}{{EF}^{2}}$，
∴EF²=$\frac{{a}^{2}{+b}^{2}}{2}$，
∵EF＞0
∴EF=$\frac{\sqrt{{a}^{2}{+b}^{2}}}{2}$．

点评 本题考查了相似三角形的性质的应用，是一道中档题．