
分析 (1)设出M的坐标,根据中点坐标公式以及两垂直直线的斜率的关系得到方程组,解出即可;
(2)设出B的坐标,根据直线y=2x和直线AB的夹角是45°,结合两角和的正切公式求出B的坐标即可;
(3)设出C的坐标,根据|BC|的长是2$\sqrt{10}$,以及直线KAB•KBC=-1,从而求出C点的坐标即可.
解答 解:(1)设M(a,b),
则$\left\{\begin{array}{l}{\frac{b-1}{a-3}=-\frac{1}{2}}\\{\frac{a+3}{2}•2=\frac{b+1}{2}}\end{array}\right.$,
解得:a=-$\frac{11}{3}$,b=-$\frac{7}{3}$,
即M(-$\frac{11}{3}$,-$\frac{7}{3}$);
(2)由题意得B点在直线y=2x上,
设B(m,2m),
∴直线AB的斜率是:KAB=$\frac{2m-1}{m-3}$,
∴tan(arctan2+$\frac{π}{4}$)=$\frac{2m-1}{m-3}$或tan(arctan2-$\frac{π}{4}$)=$\frac{2m-1}{m-3}$,
解得:B(2,4)或(0,0),
(3)由(2)得:B(2,4),
设BC的距离是h,则$\frac{1}{2}$•$\sqrt{10}$•h=10,解得:h=2$\sqrt{10}$,
设C(x,y),则$\frac{4-y}{2-x}•\frac{4-1}{3-2}$=-1,得:x-3y+10=0①,
又|BC|=$\sqrt{{(x-2)}^{2}{+(y-4)}^{2}}$=2$\sqrt{10}$②,
由①②得:C(6,8)或(2,-4),
故过A(3,1),C(6,8)的直线为:
7x-3y-18=0,
过A(3,1),C(2,-4)的直线为:
5x-y-14=0.
点评 本题考查了两点间的距离公式,考查直线斜率的求法以及求直线方程问题,是一道中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
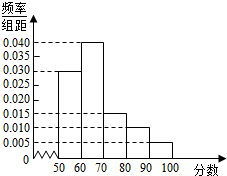 根据某组调查数据制作的频率分布直方图如图所示,则该组数据中的数位于区间(60,70)内的频率是( )
根据某组调查数据制作的频率分布直方图如图所示,则该组数据中的数位于区间(60,70)内的频率是( )| A. | 0.004 | B. | 0.04 | C. | 0.4 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,2} | B. | {1,2} | C. | {0} | D. | 以上答案都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知抛物线C1:y2=2px(p>0)上一点Q(1,a)到焦点的距离为3,
已知抛物线C1:y2=2px(p>0)上一点Q(1,a)到焦点的距离为3,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | -$\frac{1}{7}$ | D. | -$\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com