
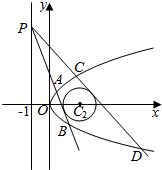
 已知抛物线C1:y2=2px(p>0)上一点Q(1,a)到焦点的距离为3,
已知抛物线C1:y2=2px(p>0)上一点Q(1,a)到焦点的距离为3,分析 (Ⅰ)根据抛物线的定义即可得到$1+\frac{p}{2}=3$,求出p=4,从而焦点坐标为(2,0),这便得到$\sqrt{1+{a}^{2}}=3$,从而可求出a的值;
(Ⅱ)可设过点P的直线l方程为:y-y0=k(x+1),联立抛物线方程消去x便可得到ky2-8y+8y0+8k=0,可设直线AB,CD的斜率分别为k1,k2,A,B,C,D四点的纵坐标分别为y1,y2,y3,y4,从而可以得到${y}_{1}{y}_{2}=\frac{8({y}_{0}+{k}_{1})}{{k}_{1}},{y}_{3}{y}_{4}=\frac{8({y}_{0}+{k}_{2})}{{k}_{2}}$.可以求圆心C2到切线l的距离,从而可以得到关于k的一元二次方程,由韦达定理得到k1+k2=-y0,这样即可求得y1y2y3y4=64,即得出A,B,C,D四点纵坐标之积为定值.
解答 解:(Ⅰ)根据抛物线的定义,Q(1,a)到准线x=$-\frac{p}{2}$的距离为3;
∴$1+\frac{p}{2}=3$;
∴p=4;
∴抛物线的焦点坐标为(2,0);
∴$\sqrt{1+{a}^{2}}=3$;
∴$a=±2\sqrt{2}$;
(Ⅱ)设P(-1,y0),过点P的直线方程设为l:y-y0=k(x+1);
由$\left\{\begin{array}{l}{{y}^{2}=8x}\\{y-{y}_{0}=k(x+1)}\end{array}\right.$得,ky2-8y+8y0+8k=0;
若直线AB,CD的斜率分别为k1,k2,设A,B,C,D的纵坐标分别为y1,y2,y3,y4;
∴${y}_{1}{y}_{2}=\frac{8({y}_{0}+{k}_{1})}{{k}_{1}},{y}_{3}{y}_{4}=\frac{8({y}_{0}+{k}_{2})}{{k}_{2}}$;
∵C2到l的距离d=$\frac{|3k+{y}_{0}|}{\sqrt{1+{k}^{2}}}=\sqrt{3}$;
∴$6{k}^{2}+6{y}_{0}k+{{y}_{0}}^{2}-3=0$;
∴${k}_{1}+{k}_{2}=-{y}_{0},{k}_{1}{k}_{2}=\frac{{{y}_{0}}^{2}-3}{6}$;
∴${y}_{1}{y}_{2}{y}_{3}{y}_{4}=\frac{64[{k}_{1}{k}_{2}+({k}_{1}+{k}_{2}){y}_{0}+{{y}_{0}}^{2}]}{{k}_{1}{k}_{2}}$=$\frac{64({k}_{1}{k}_{2}-{{y}_{0}}^{2}+{{y}_{0}}^{2})}{{k}_{1}{k}_{2}}=64$;
∴A,B,C,D四点纵坐标之积为定值,且定值为64.
点评 考查抛物线的定义,抛物线的标准方程,抛物线的焦点及准线方程,两点间距离公式,直线的点斜式方程,以及韦达定理,圆心到切线距离和圆半径的关系,点到直线的距离公式.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{23}{3}$ | D. | $\frac{22}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
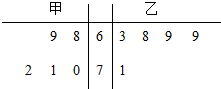 甲、乙两名同学五次数学测试的成绩统计用茎叶图表示(如图),则下列说法中正确的个数是( )
甲、乙两名同学五次数学测试的成绩统计用茎叶图表示(如图),则下列说法中正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 赞成改革 | 不赞成改革 | 无所谓 | |
| 教师 | 120 | y | 40 |
| 学生 | x | z | 130 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.60.7<0.70.6<log0.76 | B. | 0.60.7<log0.76<0.70.6 | ||
| C. | log0.76<0.60.7<0.70.6 | D. | log0.76<0.70.6<0.60.7 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
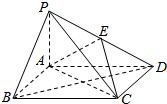 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,AP=1,AD=$\sqrt{3}$,PA⊥平面ABCD,E为PD的中点.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,AP=1,AD=$\sqrt{3}$,PA⊥平面ABCD,E为PD的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com