
分析 (Ⅰ)确定直线l恒过定点(1,1),定点(1,1)在圆内,即可证明直线l与圆C相交;
(Ⅱ)设AB中点M(x,y),当AB斜率存在时,由KAB•KCM=-1,可得$\frac{y-1}{x-1}•\frac{y-1}{x-0}$=-1,化简可得AB中点M的轨迹方程;当AB的斜率不存在时,点M的坐标也满足此轨迹方程,从而得出结论.
解答 (Ⅰ)证明:∵直线l的方程为mx-y+1-m=0,
∴m(x-1)-y+1=0,
令x-1=0,-y+1=0,∴x=1,y=1,
∴直线l恒过定点(1,1),
∴12+(1-1)2=1<5,
∴定点(1,1)在圆内,
∴直线l与圆C相交;
(Ⅱ)设AB中点M(x,y),当AB的斜率存在时,由题意可得CM⊥AB,故有KAB•KCM=-1.
∴$\frac{y-1}{x-1}•\frac{y-1}{x-0}$=-1,化简可得(x-$\frac{1}{2}$)2+(y-1)2=$\frac{1}{4}$,
即AB中点M的轨迹方程为(x-$\frac{1}{2}$)2+(y-1)2=$\frac{1}{4}$.
当AB的斜率不存在时,直线AB的方程为x=1,此时AB的中点M的坐标为(1,1),
也满足(x-$\frac{1}{2}$)2+(y-1)2=$\frac{1}{4}$.
综上可得,AB中点M的轨迹方程为(x-$\frac{1}{2}$)2+(y-1)2=$\frac{1}{4}$.
点评 本题主要考查直线和圆的位置关系的判定,直线过定点问题,求点的轨迹方程,属于中档题.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | f(x)=ax2+bx+c | B. | f(x)=aex+b | C. | f(x)=eax+b | D. | f(x)=alnx+b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
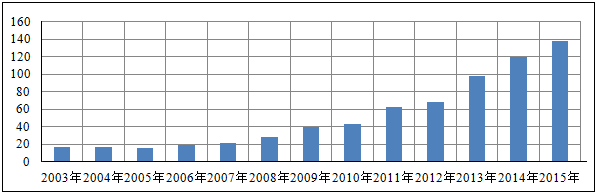
| x | 3 | 4 | 5 | 6 | 8 | 10 |
| y | 40 | 45 | 60 | 55 | 70 | 90 |
| A. | 79.8 | B. | 96.6 | C. | 83.1 | D. | 69.7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
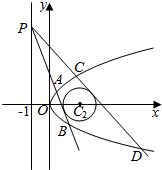 已知抛物线C1:y2=2px(p>0)上一点Q(1,a)到焦点的距离为3,
已知抛物线C1:y2=2px(p>0)上一点Q(1,a)到焦点的距离为3,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 恰有1名男生与恰有2名女生 | B. | 至少有1名男生与全是男生 | ||
| C. | 至少有1名男生与至少有1名女生 | D. | 至少有1名男生与全是女生 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com