
分析 先求出满足f(x)≥3的x的范围,再求出t=$\frac{x+1}{x-1}$的范围,结合对数函数的图象和性质,可得答案.
解答 解:当x≤0时,由2-x-1≥3得:x≤-2,
当x>0时,由${{x}^{\frac{1}{2}}}_{\;}$≥3得:x≥9,
故t=$\frac{x+1}{x-1}$=1+$\frac{2}{x-1}$∈[$\frac{1}{3}$,1)∪(1,$\frac{5}{4}$],
故log2($\frac{x+1}{x-1}$)的最大值为log2$\frac{5}{4}$,
故答案为:log2$\frac{5}{4}$
点评 本题考查的知识点是分段函数的应用,反比例型函数的图象和性质,对数函数的图象和性质,难度中档.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 为了检查某高三毕业班学生的体重状况,从该班随机抽取了10位学生进行称重,如图为10位学生体重的茎叶图,其中图中左边是体重的十位数字,右边是个位数字,则这10位学生体重的平均数与中位数之差为( )( )
为了检查某高三毕业班学生的体重状况,从该班随机抽取了10位学生进行称重,如图为10位学生体重的茎叶图,其中图中左边是体重的十位数字,右边是个位数字,则这10位学生体重的平均数与中位数之差为( )( )| A. | 0.1 | B. | 0.2 | C. | 0.3 | D. | 0.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+y2+2x+3y+5=0 | B. | x2+y2+2x+3y+6=0 | C. | x2+y2+2x+3y+3=0 | D. | x2+y2+2x+3y+4=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
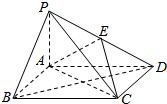 如图,四棱锥P-ABCD中,底面ABCD为平行四边形,AP=1,AD=$\sqrt{3}$,PA⊥平面ABCD,E为PD的中点.
如图,四棱锥P-ABCD中,底面ABCD为平行四边形,AP=1,AD=$\sqrt{3}$,PA⊥平面ABCD,E为PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{10}{3}$ | B. | -$\frac{2}{3}$ | C. | 0 | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 气温y(℃) | 18 | 16 | 10 | 4 | 2 |
| 山高(km) | 2.6 | 3 | 3.4 | 4.2 | 4.8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 25件 | B. | 20件 | C. | 15件 | D. | 30件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com