
| A. | 25件 | B. | 20件 | C. | 15件 | D. | 30件 |
分析 分析题目数据建立数学模型,得出总利润函数L(x)=$\frac{500}{\sqrt{x}}$•x-(1200+$\frac{2}{75}$x3)(x>0),注意定义域,然后利用导数求其最值,还原为实际问题即可.
解答 解:解:设产品单价为p,则有p2=$\frac{k}{x}$,
将x=100,p=50代入,得k=250000,
所以p=p(x)=$\frac{500}{\sqrt{x}}$,
设总利润为L,L=L(x)=p(x)-c(x)=$\frac{500}{\sqrt{x}}$•x-(1200+$\frac{2}{75}$x3)(x>0),
即L(x)=$\frac{500}{\sqrt{x}}$•x-1200-$\frac{2}{75}$x3,L'(x)=$\frac{250}{\sqrt{x}}$-$\frac{2{x}^{2}}{25}$,
令L'(x)=0,即$\frac{250}{\sqrt{x}}$-$\frac{2{x}^{2}}{25}$=0,解得x=25,
因为x=25是函数L(x)在(0,+∞)上唯一的极值点,
且是极大值点,从而是最大值点.
故选:A.
点评 本题考查利用导数解决生活中的优化问题的方法和步骤,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
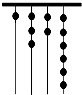 原始社会时期,人们通过在绳子上打结来计算数量,即“结绳计数”,当时有位父亲,为了准确记录孩子的成长天数,在粗细不同的绳子上打结,由细到粗,满七进一,那么孩子已经出生多少天?( )
原始社会时期,人们通过在绳子上打结来计算数量,即“结绳计数”,当时有位父亲,为了准确记录孩子的成长天数,在粗细不同的绳子上打结,由细到粗,满七进一,那么孩子已经出生多少天?( )| A. | 1326 | B. | 510 | C. | 429 | D. | 336 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com