练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
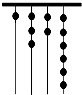
    12．原始社会时期，人们通过在绳子上打结来计算数量，即“结绳计数”，当时有位父亲，为了准确记录孩子的成长天数，在粗细不同的绳子上打结，由细到粗，满七进一，那么孩子已经出生多少天？（　　）
    A．1326B．510C．429D．336

    分析 由题意可得，该表示为七进制，运用进制转换，即可得到所求的十进制数．

    解答 解：由题意满七进一，可得该图示为七进制数，
    化为十进制数为1×73+3×72+2×7+6=510．
    故选：B．

    点评 本题考查计数的方法，注意运用七进制转化为十进制数，考查运算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    2．登山运动是一项有益身心健康的活动，但它受山上气温的限制．某登山爱好者为了了解某山上气温y（℃）与相应山高x（km）之间的关系，随机统计了5次山上气温与相应山高，如下表：
    气温y（℃）18161042
    山高（km）2.633.44.24.8
    （1）根据上表数据，用最小二乘法求出y关于x的线性回归方程：$\widehat{y}$=bx+$\widehat{a}$；
    （2）若该名登山者携带物品足以应对山上-2.4℃的环境，试根据（1）中求出的线性回归方程预测，这名登山者最高可以攀登到多少千米处？
    （参考公式：$\widehat{b}$=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{i}（{x}_{n}-\overline{x}）^{2}}$，$\widehat{a}$=$\widehat{y}$-$\widehat{b}$$\overline{x}$）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．某厂生产某种新产品x件的总成本：C（x）=1200+$\frac{2}{75}$x3，又产品单价的平方与产品件数x成反比，生产100件这样的产品的单价为50元，总利润最大时，产量应定为（　　）
    A．25件B．20件C．15件D．30件

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知平面向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1，|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{c}$|=|$\overrightarrow{b}$-$\overrightarrow{c}$|，则|$\overrightarrow{c}$|的最大值为（　　）
    A．2$\sqrt{3}$B．2C．$\sqrt{3}$D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．若A、B、C是△ABC的三个内角，则（　　）
    A．sinA=sin（B+C）B．cosA=cos（B+C）C．tanA=tan（B+C）D．cotA=cot（B+C）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    17．在△ABC中，a=4，b=4，C=30°，则c2等于（　　）
    A．32-16$\sqrt{3}$B．32+16$\sqrt{3}$C．16D．48

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．若△ABC外接圆直径为2，A=75°，B=45°，则△ABC的面积为$\frac{3+\sqrt{3}}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．设Sn为等差数列{an}的前n项和，其中a1=1，且$\frac{{S}_{n}}{{a}_{n}}$=λan+1（n∈N*），记bn=$\frac{{a}_{n}}{{3}^{{a}_{n}}}$，数列{bn}的前n项和为Tn，若对任意的n∈N*，都有Tn＜m成立，则m的取值范围为[$\frac{3}{4}$，+∞）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．2015年9月3日，抗战胜利70周年纪念日放假期间，某办公室中的8位同事计划分两组（每组4人）分别从A、B、C、D四个革命教育基地中选取一个参观学习，两组不去同一地点，已知甲不愿意去A地，乙不愿意去B，C两地，则不同的分组参观方式共有（　　）
    A．280B．145C．140D．122

    查看答案和解析>>

    同步练习册答案