
分析 求得a2,a3,再由a1,a2,a3成等差数列,解得λ=$\frac{1}{2}$.求得等差数列{an}的公差为1,an=1+n-1=n,Sn=$\frac{1}{2}$n(1+n),再由数列的求和方法:错位相减法,以及不等式成立问题的解法,即可得到所求范围.
解答 解:n=1时,$\frac{{S}_{1}}{{a}_{1}}$=λa2,解得a2=$\frac{1}{λ}$;
n=2时,$\frac{{S}_{2}}{{a}_{2}}$=λa3,即$\frac{1+\frac{1}{λ}}{\frac{1}{λ}}$=λa3,
解得a3=1+$\frac{1}{λ}$.
由1,$\frac{1}{λ}$,1+$\frac{1}{λ}$成等差数列,可得
2+$\frac{1}{λ}$=$\frac{2}{λ}$,解得λ=$\frac{1}{2}$.
则等差数列{an}的公差为1,an=1+n-1=n,
Sn=$\frac{1}{2}$n(1+n),$\frac{{S}_{n}}{{a}_{n}}$=$\frac{1}{2}$(1+n)=λan+1恒成立,
则bn=$\frac{{a}_{n}}{{3}^{{a}_{n}}}$=n•($\frac{1}{3}$)n,
Tn=1•$\frac{1}{3}$+2•($\frac{1}{3}$)2+3•($\frac{1}{3}$)3+…+n•($\frac{1}{3}$)n,
$\frac{1}{3}$Tn=1•($\frac{1}{3}$)2+2•($\frac{1}{3}$)3+3•($\frac{1}{3}$)4+…+n•($\frac{1}{3}$)n+1,
相减可得,$\frac{2}{3}$Tn=$\frac{1}{3}$+($\frac{1}{3}$)2+($\frac{1}{3}$)3+…+($\frac{1}{3}$)n-n•($\frac{1}{3}$)n+1
=$\frac{\frac{1}{3}(1-\frac{1}{{3}^{n}})}{1-\frac{1}{3}}$-n•($\frac{1}{3}$)n+1,
化简可得Tn=$\frac{3}{4}$-$\frac{2n+3}{4•{3}^{n}}$,
由$\frac{2n+3}{4•{3}^{n}}$>0,可得Tn<$\frac{3}{4}$,
由Tn<m恒成立,可得m≥$\frac{3}{4}$.
故答案为:[$\frac{3}{4}$,+∞).
点评 本题考查等差数列的通项公式和求和公式的运用,考查不等式恒成立问题的解法,以及数列的求和方法:错位相减法,考查化简整理的圆能力,属于中档题.


科目:高中数学 来源: 题型:选择题
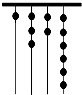 原始社会时期,人们通过在绳子上打结来计算数量,即“结绳计数”,当时有位父亲,为了准确记录孩子的成长天数,在粗细不同的绳子上打结,由细到粗,满七进一,那么孩子已经出生多少天?( )
原始社会时期,人们通过在绳子上打结来计算数量,即“结绳计数”,当时有位父亲,为了准确记录孩子的成长天数,在粗细不同的绳子上打结,由细到粗,满七进一,那么孩子已经出生多少天?( )| A. | 1326 | B. | 510 | C. | 429 | D. | 336 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,抛物线y2=4x的焦点为F,动点T(-1,m),过F作TF的垂线交抛物线于P,Q两点,弦PQ的中点为N.
如图所示,抛物线y2=4x的焦点为F,动点T(-1,m),过F作TF的垂线交抛物线于P,Q两点,弦PQ的中点为N.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | -$\frac{3}{2}$ | C. | ±$\frac{3}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com