Question

20．已知平面向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$满足|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1，|$\overrightarrow{a}$-$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{c}$|=|$\overrightarrow{b}$-$\overrightarrow{c}$|，则|$\overrightarrow{c}$|的最大值为（　　）

• A． 2$\sqrt{3}$
• B． 2
• C． $\sqrt{3}$
• D． 1

Answer 1

分析 作向量$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，设向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为α，由三角形的全等可得OC垂直平分AB，设AB=t，t=2sin$\frac{α}{2}$，
即有|$\overrightarrow{c}$|=cos$\frac{α}{2}$+$\sqrt{3}$sin$\frac{α}{2}$=2sin（$\frac{α}{2}$+$\frac{π}{6}$），再由正弦函数的值域，即可得到所求最大值．

解答 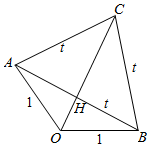解：作向量$\overrightarrow{OA}$=$\overrightarrow{a}$，$\overrightarrow{OB}$=$\overrightarrow{b}$，$\overrightarrow{OC}$=$\overrightarrow{c}$，
设向量$\overrightarrow{a}$，$\overrightarrow{b}$的夹角为α，
由题意可得OA=OB，CA=CB=AB，
可得△CAO≌△CBO，
即有OC垂直平分AB，
设AB=t，t=2sin$\frac{α}{2}$，
等边三角形ABC的高CH为$\frac{\sqrt{3}}{2}$•t=$\sqrt{3}$sin$\frac{α}{2}$，
则|$\overrightarrow{c}$|=cos$\frac{α}{2}$+$\sqrt{3}$sin$\frac{α}{2}$=2sin（$\frac{α}{2}$+$\frac{π}{6}$），
当$\frac{α}{2}$+$\frac{π}{6}$=$\frac{π}{2}$，即α=$\frac{2π}{3}$时，取得最大值，且为2．
故选：B．

点评 本题考查向量的模的最值的求法，注意运用向量的加减运算和三角函数的化简和求值，以及正弦函数的值域，属于中档题．