
【题目】已知函数f(x)=lnx﹣ ![]() (m∈R)在区间[1,e]取得最小值4,则m= .
(m∈R)在区间[1,e]取得最小值4,则m= .
【答案】﹣3e
【解析】解:函数 ![]() 的定义域为(0,+∞),
的定义域为(0,+∞),
![]() .
.
当f′(x)=0时, ![]() ,此时x=﹣m,如果m≥0,则无解.
,此时x=﹣m,如果m≥0,则无解.
所以,当m≥0时,f′(x)>0,f(x)为增函数,所以f(x)min=f(1)=﹣m=4,m=﹣4,矛盾舍去;
当m<0时,
若x∈(0,﹣m),f′(x)<0,f(x)为减函数,若x∈(﹣m,+∞),f′(x)>0,f(x)为增函数,
所以f(﹣m)=ln(﹣m)+1为极小值,也是最小值;
①当﹣m<1,即﹣1<m<0时,f(x)在[1,e]上单调递增,所以f(x)min=f(1)=﹣m=4,所以m=﹣4(矛盾);
②当﹣m>e,即m<﹣e时,f(x)在[1,e]上单调递减,f(x)min=f(e)=1﹣ ![]() =4.所以m=﹣3e.
=4.所以m=﹣3e.
③当﹣1≤﹣m≤e,即﹣e≤m≤1时,f(x)在[1,e]上的最小值为f(﹣m)=ln(﹣m)+1=4.此时m=﹣e3<﹣e(矛盾).
综上m=﹣3e.
求出函数的导函数,然后分m的范围讨论函数的单调性,根据函数的单调性求出函数的最小值,利用最小值等于4求m的值.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)若曲线y=f(x)在P(1,f(1))处的切线平行于直线y=﹣x+1,求函数y=f(x)的单调区间;
(2)若a>0,且对任意x∈(0,2e]时,f(x)>0恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角梯形ABCD中,AB⊥AD,AD∥BC,AB=BC=2AD=2,E,F分别为BC,CD的中点,以A为圆心,AD为半径的圆交AB于G,点P在 ![]() 上运动(如图).若
上运动(如图).若 ![]() =λ
=λ ![]() +μ
+μ ![]() ,其中λ,μ∈R,则6λ+μ的取值范围是( )
,其中λ,μ∈R,则6λ+μ的取值范围是( ) 
A.[1, ![]() ]
]
B.[ ![]() ,2
,2 ![]() ]
]
C.[2,2 ![]() ]
]
D.[1,2 ![]() ]
]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥 ![]() 中,平面PAD⊥ABCD,AB=AD,∠BAD=60°,E,F分别是AP,AD的中点.
中,平面PAD⊥ABCD,AB=AD,∠BAD=60°,E,F分别是AP,AD的中点.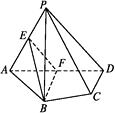
求证:
(1)直线EF∥平面PCD;
(2)平面BEF⊥平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设命题p:x0∈(0,+∞),3 ![]() +x0=2016,命题q:a∈(0,+∞),f(x)=|x|﹣ax,(x∈R)为偶函数,那么,下列命题为真命题的是( )
+x0=2016,命题q:a∈(0,+∞),f(x)=|x|﹣ax,(x∈R)为偶函数,那么,下列命题为真命题的是( )
A.p∧q
B.(¬p)∧q
C.p∧(¬q)
D.(¬p)∧(¬q)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线方程为16x2﹣9y2=144.
(1)求该双曲线的实轴长、虚轴长、离心率;
(2)若抛物线C的顶点是该双曲线的中心,而焦点是其左顶点,求抛物线C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数y=f(x)对任意的x∈(﹣ ![]() ,
, ![]() )满足f′(x)cosx+f(x)sinx>0(其中f′(x)是函数f(x)的导函数),则下列不等式成立的是 . ①
)满足f′(x)cosx+f(x)sinx>0(其中f′(x)是函数f(x)的导函数),则下列不等式成立的是 . ① ![]() f(﹣
f(﹣ ![]() )<f(﹣
)<f(﹣ ![]() )
)
② ![]() f(
f( ![]() )<f(
)<f( ![]() )
)
③f(0)>2f( ![]() )
)
④f(0)> ![]() f(
f( ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设b和c分别是先后抛掷一枚骰子得到的点数,用随机变量ξ表示方程x2+bx+c=0实根的个数(重根按一个计).
(1)求方程x2+bx+c=0有实根的概率;
(2)(理)求ξ的分布列和数学期望 (文)求P(ξ=1)的值
(3)(理)求在先后两次出现的点数中有5的条件下,方程x2+bx+c=0有实根的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com