练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在5道题中有3道理科题和2道文科题.如果不放回地依次抽取2 道题，求：

    (l）第1次抽到理科题的概率；

    (2）第1次和第2次都抽到理科题的概率；

    (3）在第 1 次抽到理科题的条件下，第2次抽到理科题的概率．

    【答案】(1)(2）(3）

    【解析】本题考查了有条件的概率的求法，做题时要认真分析，找到正确方法．（1）因为有5件是次品，第一次抽到理科试题，有3中可能，试题共有5件，（2）因为是不放回的从中依次抽取2件，所以第一次抽到理科题有5种可能，第二次抽到理科题有4种可能，第一次和第二次都抽到理科题有6种可能，总情况是先从5件中任抽一件，再从剩下的4件中任抽一件，所以有20种可能，再令两者相除即可．

    （3）因为在第1次抽到理科题的条件下，第2次抽到文科题的概率为

    （1）；……….5分

    （2）；………5分

    （3）．……….5分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知集合M＝{x|x<－3，或x>5}，P＝{x|(x－a)·(x－8)≤0}．

    (1)求M∩P＝{x|5<x≤8}的充要条件；

    (2)求实数a的一个值，使它成为M∩P＝{x|5<x≤8}的一个充分但不必要条件．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在三棱柱ABC﹣A1B1C1中，已知AB=AC=AA1= ，BC=4，点A1在底面ABC的投影是线段BC的中点O．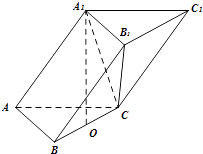

    （1）证明在侧棱AA1上存在一点E，使得OE⊥平面BB1C1C，并求出AE的长；
    （2）求平面A1B1C与平面BB1C1C夹角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，已知 ．
    （1）求证：tanB=3tanA；
    （2）若cosC= ，求A的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，建立平面直角坐标系xOy，x轴在地平面上，y轴垂直于地平面，单位长度为1千米．某炮位于坐标原点．已知炮弹发射后的轨迹在方程y=kx﹣ （1+k2）x2（k＞0）表示的曲线上，其中k与发射方向有关．炮的射程是指炮弹落地点的横坐标．

    （1）求炮的最大射程；
    （2）设在第一象限有一飞行物（忽略其大小），其飞行高度为3.2千米，试问它的横坐标a不超过多少时，炮弹可以击中它？请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知各项均为正数的两个数列{an}和{bn}满足：an+1= ，n∈N* ，
    （1）设bn+1=1+ ，n∈N*，求证：数列{ }是等差数列；
    （2）设bn+1= ，n∈N*，且{an}是等比数列，求a1和b1的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设某大学的女生体重y（单位：kg）与身高x（单位：cm）具有线性相关关系，根据一组样本数据（xi ， yi）（i=1，2，…，n），用最小二乘法建立的回归方程为 =0.85x﹣85.71，则下列结论中不正确的是（ ）
    A.y与x具有正的线性相关关系
    B.回归直线过样本点的中心（ ， ）
    C.若该大学某女生身高增加1cm，则其体重约增加0.85kg
    D.若该大学某女生身高为170cm，则可断定其体重必为58.79kg

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱中，底面，，，，分别为的中点，为侧棱上的动点

    （Ⅰ）求证：平面平面；

    （Ⅱ）若为线段的中点，求证：平面；

    （Ⅲ）试判断直线与平面是否能够垂直。若能垂直，求的值；若不能垂直，请说明理由

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了在夏季降温和冬季供暖时减少能源损耗，房屋的屋顶和外墙需要建造隔热层.某幢建筑物要建造可使用年的隔热层，每厘米厚的隔热层建造成本为万元.该建筑物每年的能源消耗费用（单位：万元）与隔热层厚度（单位：厘米）满足关系：.若不建隔热层，每年的能源消耗费用为万元.设为隔热层建造费用与年的能源消耗费用之和.

    （1）求的值及的表达式；

    （2）隔热层修建多厚时，总费用最小，并求其最小值.

    查看答案和解析>>

    同步练习册答案