Question

【题目】已知各项均为正数的两个数列{an}和{bn}满足：an+1= ，n∈N* ，
（1）设bn+1=1+ ，n∈N*，求证：数列{ }是等差数列；
（2）设bn+1= ，n∈N*，且{an}是等比数列，求a1和b1的值．

Answer 1

【答案】
（1）解：由题意可知，an+1= = =

∴

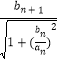
从而数列{ }是以1为公差的等差数列

（2）解：∵an＞0，bn＞0

∴

从而 （*）

设等比数列{an}的公比为q，由an＞0可知q＞0

下证q=1

若q＞1，则 ，故当 时， 与（*）矛盾

0＜q＜1，则 ，故当 时， 与（*）矛盾

综上可得q=1，an=a1，

所以，

∵

∴数列{bn}是公比 的等比数列

若 ，则 ，于是b1＜b2＜b3

又由 可得

∴b1，b2，b3至少有两项相同，矛盾

∴ ，从而 =

∴

【解析】（1）由题意可得，an+1= = = 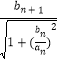，从而可得 ，可证（2）由基本不等式可得， ，由{an}是等比数列利用反证法可证明q= =1，进而可求a1 ， b1
【考点精析】解答此题的关键在于理解等差关系的确定的相关知识，掌握如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，即－=d ，（n≥2，n∈N）那么这个数列就叫做等差数列，以及对等比数列的基本性质的理解，了解{an}为等比数列，则下标成等差数列的对应项成等比数列;{an}既是等差数列又是等比数列== {an}是各项不为零的常数列．