
分析 根据A(1,3),B(3,1),求出AB的直线方程,和AB的距离,利用点到直线的距离就是AB为底的高,即可得△ABC 的面积.
解答 解:由A(1,3),B(3,1),
设AB的直线方程为y=kx+b,
则$\left\{\begin{array}{l}{3=k+b}\\{1=3k+b}\end{array}\right.$,
解得:k=-1,b=4.
AB的直线方程为x+y-4=0.
C(-1,0)到直线AB的距离h=$\frac{|-1-4|}{\sqrt{2}}=\frac{5}{\sqrt{2}}$.
AB的距离d=$\sqrt{(3-1)^{2}+(3-1)^{2}}$=2$\sqrt{2}$.
则△ABC 的面积S=$\frac{1}{2}$×$\frac{5}{\sqrt{2}}×2\sqrt{2}$=5.
故答案为:5.
点评 本题此解法用了点与直线的性质,两点之间的距离公式.属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
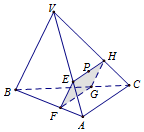 如图所示,在四面体VABC木块中,P为△VAC的重心,这点P作截面EFGH,若截面EFGH是平行四边形,则该截面把木块分成两部分体积之比为$\frac{7}{20}$. (埴体积小与体积大之比)
如图所示,在四面体VABC木块中,P为△VAC的重心,这点P作截面EFGH,若截面EFGH是平行四边形,则该截面把木块分成两部分体积之比为$\frac{7}{20}$. (埴体积小与体积大之比)查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 目的地/频数/运输时间 | 1 | 2 | 3 | 4 | 5 |
| 甲地 | 2 | 4 | 3 | 1 | |
| 乙地 | 1 | 3 | 4 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $g(x)=sin(4x+\frac{π}{6})$ | B. | $g(x)=sin(4x-\frac{π}{3})$ | C. | $g(x)=sin(2x+\frac{π}{6})$ | D. | g(x)=sin2x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
| A. | 10万元 | B. | 11万元 | C. | 12万元 | D. | 13万元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com