
分析 (1)由f′(x)=ex-1,利用导数性质能讨论f(x)的单调性.
(2)令g(x)=ex-1-x-ax2,则?x≥0,有g(x)≥0,由g(0)=0,得?m>0,使得g(x)在(0,m)上单调递增,由此能求出a的取值范围.
解答 解:(1)∵f(x)=ex-x,
∴f′(x)=ex-1,
当x>0时,f′(x)>0,∴f(x)在(0,+∞)上单调递增,
当x<0时,f′(x)<0,∴f(x)在(-∞,0)上单调递减.
(2)∵对?x≥0,恒有f(x)≥ax2+1,
∴ex-x-ax2-1≥0,
令g(x)=ex-1-x-ax2,则?x≥0,有g(x)≥0,
∵g(0)=0,∴?m>0,使得g(x)在(0,m)上单调递增,
∴在(0,t)上,g''(0)=1-2a≥0,解得a$≤\frac{1}{2}$.
下面证明:当a$≤\frac{1}{2}$时,?x≥0,恒有g(x)≥0.
证明:由(1)得?x≥0,有f(x)≥f(0)=0,
∴当x∈[0,+∞)时,ex-1≥x,且仅当x=0时,等号成立,
∴当x≥0时,g′(x)=ex-1-2ax≥x-2ax=2x($\frac{1}{2}-a$)≥0,
且仅当x=0时,等号成立,
∴g(x)在[0,+∞)递增,
∴当x∈[0,+∞)时,g(x)≥g(0)=0.
综上,a的取值范围是(-∞,$\frac{1}{2}$].
点评 本题考查函数的单调性质的讨论,考查实数的取值范围的求法,是中档题,解题时要认真审题,注意导数性质的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | $[{\sqrt{3},2}]$ | C. | $(-∞,-2)∪[{\sqrt{3},2}]$ | D. | $({-∞,-\sqrt{3}}]∪[{\sqrt{3},2}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四边形ABCD中,AD⊥AB,DC∥AB,$AD=AE=DC=\frac{1}{2}AB=4$,△MDC是等边三角形,且平面MDC⊥平面ABCD.
如图,在四边形ABCD中,AD⊥AB,DC∥AB,$AD=AE=DC=\frac{1}{2}AB=4$,△MDC是等边三角形,且平面MDC⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
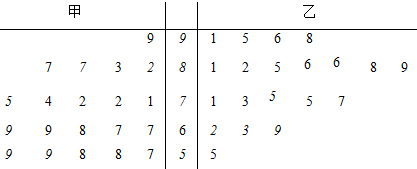
| 甲班 | 乙班 | 合计 | |
| 优秀 | |||
| 不优秀 | |||
| 合计 | 40 |
| P(χ2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
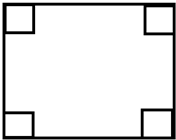 用一边长为1米,另一边长为a(0<a≤1)米的矩形铁皮做一个无盖的容器,先在四角分别截去一个长为x的小正方形,然后把四边翻折90°角,再焊接而成,设该容器的容积为f(x).
用一边长为1米,另一边长为a(0<a≤1)米的矩形铁皮做一个无盖的容器,先在四角分别截去一个长为x的小正方形,然后把四边翻折90°角,再焊接而成,设该容器的容积为f(x).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 4 | C. | $\sqrt{15}$ | D. | $\sqrt{14}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com