
分析 根据条件容易求出$\overrightarrow{a},\overrightarrow{b}$的夹角为60°,然后作$\overrightarrow{OA}=\overrightarrow{a},\overrightarrow{OB}=\overrightarrow{b}$,$\overrightarrow{OC}=\overrightarrow{c}$,结合条件从而得出∠AOB=60°,∠ACB=120°,这便说明A,O,B,C四点共圆,从而可知OC为圆的直径时$|\overrightarrow{c}|$最大,可设OC=c,结合图形及条件即可表示出cos∠AOC,cos∠BOC,sin∠AOC,sin∠BOC,而∠AOC+∠BOC=60°,这样根据两角和的余弦公式即可得出关于c2的方程,解出c2,从而便得出$|\overrightarrow{c}|$的最大值.
解答 解:根据条件:
$|\overrightarrow{a}|•cos<\overrightarrow{a},\overrightarrow{b}>=\sqrt{3}cos<\overrightarrow{a},\overrightarrow{b}>=\frac{\sqrt{3}}{2}$;
∴$cos<\overrightarrow{a},\overrightarrow{b}>=\frac{1}{2}$;
∴$<\overrightarrow{a},\overrightarrow{b}>=60°$;
如图,作$\overrightarrow{OA}=\overrightarrow{a},\overrightarrow{OB}=\overrightarrow{b}$,$\overrightarrow{OC}=\overrightarrow{c}$,则∠AOB=60°,∠ACB=120°;
∴A,O,B,C四点共圆;
∴OC为圆的直径时,$|\overrightarrow{c}|$最大;
设OC=c,则$BC=\sqrt{{c}^{2}-27},AC=\sqrt{{c}^{2}-3}$;
∴$cos∠AOC=\frac{\sqrt{3}}{c},cos∠BOC=\frac{3\sqrt{3}}{c}$,$sin∠AOC=\frac{\sqrt{{c}^{2}-3}}{c},sin∠BOC=\frac{\sqrt{{c}^{2}-27}}{c}$;
∴cos60°=cos(∠AOC+∠BOC)=$\frac{9}{{c}^{2}}-\frac{\sqrt{{c}^{2}-3}\sqrt{{c}^{2}-27}}{{c}^{2}}$=$\frac{1}{2}$;
解得c2=28;
∴$c=2\sqrt{7}$;
即$|\overrightarrow{c}|$的最大值等于$2\sqrt{7}$.
故答案为:$2\sqrt{7}$.
点评 考查投影的定义及计算公式,向量减法的几何意义,四点共圆的概念,以及两角和的余弦公式,三角函数的定义.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
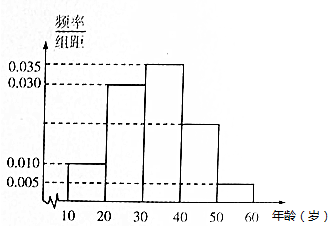 为了调查市民对某活动的认可程度,研究人员对其所在地区年龄在10~60岁间的n位市民作出调查,并将统计结果绘制成频率分布直方图如图所示,若被调查的年龄在20~30岁间的市民有480人,则可估计被调查的年龄在40~50岁间的市民有320人.
为了调查市民对某活动的认可程度,研究人员对其所在地区年龄在10~60岁间的n位市民作出调查,并将统计结果绘制成频率分布直方图如图所示,若被调查的年龄在20~30岁间的市民有480人,则可估计被调查的年龄在40~50岁间的市民有320人.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com