
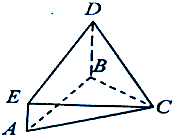
 (2011•黄冈模拟)如图,已知BD⊥平面ABC,AE∥BD,△ABC是等腰直角三角形,∠C=90°AB=BD=2AE,则面CDE与面ABC所成的角的正切值为
(2011•黄冈模拟)如图,已知BD⊥平面ABC,AE∥BD,△ABC是等腰直角三角形,∠C=90°AB=BD=2AE,则面CDE与面ABC所成的角的正切值为
| ||
| 2 |
| ||
| 2 |
| 2 |
| 10 |
| 1 | ||
|
| 4 | ||
|
| BD |
| BH |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
 (2011•黄冈模拟)已知:如图|
(2011•黄冈模拟)已知:如图|| OA |
| OB |
| OA |
| OB |
| OC |
| OA |
| OC |
| OA |
| OB |
| λ |
| μ |
查看答案和解析>>
科目:高中数学 来源: 题型:
| an |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2011•黄冈模拟)分形几何学是美籍法国数学家伯努瓦••B•曼德尔布罗特(Benoit B.Mandelbrot) 在20世纪70年代创立的一门新学科,它的创立,为解决传统科学众多领域的难题提供了全新的思路.下图按照的分形
(2011•黄冈模拟)分形几何学是美籍法国数学家伯努瓦••B•曼德尔布罗特(Benoit B.Mandelbrot) 在20世纪70年代创立的一门新学科,它的创立,为解决传统科学众多领域的难题提供了全新的思路.下图按照的分形 规律生长成一个树形图,则第10行的空心圆点的个数是( )
规律生长成一个树形图,则第10行的空心圆点的个数是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com