
【题目】设![]() 是一个由
是一个由![]() 和
和![]() 构成的
构成的![]() 行
行![]() 列的数表,且
列的数表,且![]() 中所有数字之和不小于
中所有数字之和不小于![]() ,所有这样的数表构成的集合记为
,所有这样的数表构成的集合记为![]() ,记
,记![]() 为
为![]() 的第
的第![]() 行各数之和
行各数之和![]() ,
,![]() 为
为![]() 的第
的第![]() 列各数之和
列各数之和![]() ,
,![]() 为
为![]() 、
、![]() 、
、![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中的最大值.
中的最大值.
(1)对如下数表![]() ,求
,求![]() 的值;
的值;
|
|
|
|
|
|
|
|
(2)设数表![]() ,求
,求![]() 的最小值;
的最小值;
(3)已知![]() 为正整数,对于所有的
为正整数,对于所有的![]() ,
,![]() ,且
,且![]() 的任意两行中最多有
的任意两行中最多有![]() 列各数之和为
列各数之和为![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)计算出![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 的值,根据题中定义可得出
的值,根据题中定义可得出![]() 的值;
的值;
(2)由题意知,![]() 中所有数字之和的最小值为
中所有数字之和的最小值为![]() ,则
,则![]() 中至少有
中至少有![]() 个
个![]() ,只有当每行或每列都放
,只有当每行或每列都放![]() 个
个![]() ,才能使得
,才能使得![]() 取到最小值
取到最小值![]() ,然后就某行某列分别放
,然后就某行某列分别放![]() 个
个![]() 、
、![]() 个
个![]() 、
、![]() 个
个![]() ,列举出其他
,列举出其他![]() 行(或
行(或![]() 列)
列)![]() 的个数,得出
的个数,得出![]() 的最小值,于此得出
的最小值,于此得出![]() ;
;
(3)先计算出数表![]() 中的元素之和为
中的元素之和为![]() ,由题意定义得出
,由题意定义得出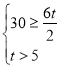 ,可得出
,可得出![]() ,然后分别就
,然后分别就![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 时就
时就![]() 的任意两行中数字之和为
的任意两行中数字之和为![]() 的列数进行分析,可得出
的列数进行分析,可得出![]() 的值.
的值.
(1)由题意可得![]() ,
,![]() ,
,
![]() ;
;
(2)由题意可得,![]() 中所有数字之和不小于
中所有数字之和不小于![]() ,即至少有
,即至少有![]() 个
个![]() .
.
而要使![]() 最小,则
最小,则![]() 中只有
中只有![]() 个
个![]() ,此时如表排列
,此时如表排列![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
下面利用来说明![]() .
.
①当某行某列全都是![]() 时,则其他
时,则其他![]() 行(或
行(或![]() 列)
列)![]() 的个数分别为:
的个数分别为:![]() 、
、![]() 、
、![]() 、
、![]() ,此时
,此时![]() ;
;
②当某行某列只放![]() 个
个![]() 时,则其他
时,则其他![]() 行(或
行(或![]() 列)
列)![]() 的个数分别为:
的个数分别为:![]() 、
、![]() 、
、![]() 、
、![]() ,则
,则![]() ;
;
③当某行过某列放![]() 个
个![]() 时,则其他
时,则其他![]() 行(或
行(或![]() 列)
列)![]() 的个数分别为:
的个数分别为:![]() 、
、![]() 、
、![]() 、
、![]() ,此时
,此时![]() .
.
由上可知,![]() ;
;
(3)![]() ,
,![]() 中所有数字之和为
中所有数字之和为![]() ,
,
由题意可得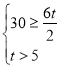 ,解得
,解得![]() .
.
①当![]() 时,每行中仅有
时,每行中仅有![]() 列为
列为![]() ,任意两行中至多有
,任意两行中至多有![]() 列和为
列和为![]() ,舍去;
,舍去;
②当![]() 时,每行中仅有
时,每行中仅有![]() 列为
列为![]() ,任意两行中至多有
,任意两行中至多有![]() 列和为
列和为![]() ,舍去;
,舍去;
③当![]() 时,如下表所示,每行中仅有
时,如下表所示,每行中仅有![]() 列为
列为![]() ,任意两行中至多有
,任意两行中至多有![]() 列和为
列和为![]() ,
,
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合乎题意;
④当![]() 或
或![]() 时,不成立.
时,不成立.
综上所述,![]() .
.


科目:高中数学 来源: 题型:
【题目】对任意![]() ,
,![]() ,
,![]() ,给出下列命题:
,给出下列命题:
①“![]() ”是“
”是“![]() ”的充要条件;
”的充要条件;
②“![]() 是无理数”是“
是无理数”是“![]() 是无理数”的充要条件;
是无理数”的充要条件;
③“![]() ”是“
”是“![]() ”的必要条件,
”的必要条件,
④“![]() ”是“
”是“![]() ”的充分条件.
”的充分条件.
其中真命题的个数为().
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据下图给出的2000年至2016年我国实际利用外资情况,以下结论正确的是

A. 2000年以来我国实际利用外资规模与年份负相关
B. 2010年以来我国实际利用外资规模逐年增加
C. 2008年我国实际利用外资同比增速最大
D. 2010年以来我国实际利用外资同比增速最大
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成![]() 两组,每组100只,其中
两组,每组100只,其中![]() 组小鼠给服甲离子溶液,
组小鼠给服甲离子溶液,![]() 组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:

记![]() 为事件:“乙离子残留在体内的百分比不低于
为事件:“乙离子残留在体内的百分比不低于![]() ”,根据直方图得到
”,根据直方图得到![]() 的估计值为
的估计值为![]() .
.
(1)求乙离子残留百分比直方图中![]() 的值;
的值;
(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,以原点为极点,以![]() 轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线
轴的非负半轴为极轴且取相同的单位长度建立极坐标系,曲线![]() 的极坐标方程为:
的极坐标方程为:![]() .
.
(1)若曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),求曲线
为参数),求曲线![]() 的直角坐标方程和曲线
的直角坐标方程和曲线![]() 的普通方程;
的普通方程;
(2)若曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),
为参数),![]() ,且曲线
,且曲线![]() 与曲线
与曲线![]() 的交点分别为
的交点分别为![]() 、
、![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知有限集![]() . 如果
. 如果![]() 中元素
中元素![]() 满足
满足![]() ,就称
,就称![]() 为“复活集”,给出下列结论:
为“复活集”,给出下列结论:
①集合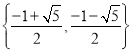 是“复活集”;
是“复活集”;
②若![]() ,且
,且![]() 是“复活集”,则
是“复活集”,则![]() ;
;
③若![]() ,则
,则![]() 不可能是“复活集”;
不可能是“复活集”;
④若![]() ,则“复活集”
,则“复活集”![]() 有且只有一个,且
有且只有一个,且![]() .
.
其中正确的结论是____________.(填上你认为所有正确的结论序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com