
【题目】设直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两个不同的点,与
两个不同的点,与![]() 轴相交于点
轴相交于点![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)证明:![]() ;
;
(2)若![]() ,求
,求![]() 的面积取得最大值时椭圆的方程.
的面积取得最大值时椭圆的方程.
【答案】(1)![]() .
.
(2)![]() 的面积取得最大值时椭圆的方程是
的面积取得最大值时椭圆的方程是![]() .
.
【解析】
(1)设直线l的方程为y=k(x+1),将直线的方程代入抛物线的方程,消去x得到关于y的一元二次方程,再结合直线l与椭圆相交于两个不同的点得到根的判别式大于0,从而解决问题;
(2)设A(x1,y1),B(x2,y2),由(1)得![]() ,由
,由![]() =3
=3![]() 得y2=
得y2=![]() ,从而求得△OAB的面积,最后利用基本不等式求得其最大值及取值最大值时的k值,从而△OAB的面积取得最大值时椭圆方程可求.
,从而求得△OAB的面积,最后利用基本不等式求得其最大值及取值最大值时的k值,从而△OAB的面积取得最大值时椭圆方程可求.
(1)依题意,直线![]() 显然不平行于坐标轴,故
显然不平行于坐标轴,故![]() 可化为
可化为![]() .
.
将![]() 代入
代入![]() ,消去
,消去![]() ,
,
得![]() ,①
,①
由直线![]() 与椭圆相交于两个不同的点,
与椭圆相交于两个不同的点,
![]() ,整理得
,整理得![]() .
.
(2)设![]() ,
,![]() .由①,得
.由①,得![]() ,
,
因为![]() ,得
,得![]() ,代入上式,得
,代入上式,得![]() .
.
于是,![]() 的面积
的面积![]() ,
,
其中,上式取等号的条件是![]() ,即
,即![]() .
.
由![]() ,可得
,可得![]() .
.
将![]() ,
,![]() 及
及![]() ,
,![]()
这两组值分别代入①,均可解出![]() .
.
所以,![]() 的面积取得最大值时椭圆的方程是
的面积取得最大值时椭圆的方程是
![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】设![]() 是一个由
是一个由![]() 和
和![]() 构成的
构成的![]() 行
行![]() 列的数表,且
列的数表,且![]() 中所有数字之和不小于
中所有数字之和不小于![]() ,所有这样的数表构成的集合记为
,所有这样的数表构成的集合记为![]() ,记
,记![]() 为
为![]() 的第
的第![]() 行各数之和
行各数之和![]() ,
,![]() 为
为![]() 的第
的第![]() 列各数之和
列各数之和![]() ,
,![]() 为
为![]() 、
、![]() 、
、![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中的最大值.
中的最大值.
(1)对如下数表![]() ,求
,求![]() 的值;
的值;
|
|
|
|
|
|
|
|
(2)设数表![]() ,求
,求![]() 的最小值;
的最小值;
(3)已知![]() 为正整数,对于所有的
为正整数,对于所有的![]() ,
,![]() ,且
,且![]() 的任意两行中最多有
的任意两行中最多有![]() 列各数之和为
列各数之和为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,底面ABCD为正方形,平面PAD⊥底面ABCD,PD⊥AD,PD=AD,E为棱PC的中点

(I)证明:平面PBC⊥平面PCD;
(II)求直线DE与平面PAC所成角的正弦值;
(III)若F为AD的中点,在棱PB上是否存在点M,使得FM⊥BD?若存在,求![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某手机生产厂商为迎接5G时代的到来,要生产一款5G手机,在生产之前,该公司对手机屏幕的需求尺寸进行社会调查,共调查了400人,将这400人按对手机屏幕的需求尺寸分为6组,分别是:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:英寸),得到如下频率分布直方图:
(单位:英寸),得到如下频率分布直方图:

其中,屏幕需求尺寸在![]() 的一组人数为50人.
的一组人数为50人.
(1)求a和b的值;
(2)用分层抽样的方法在屏幕需求尺寸为![]() 和
和![]() 两组人中抽取6人参加座谈,并在6人中选择2人做代表发言,则这2人来自同一分组的概率是多少?
两组人中抽取6人参加座谈,并在6人中选择2人做代表发言,则这2人来自同一分组的概率是多少?
(3)若以厂家此次调查结果的频率作为概率,市场随机调查两人,这两人屏幕需求尺寸分别在![]() 和
和![]() 的概率是多少?
的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论错误的是( )
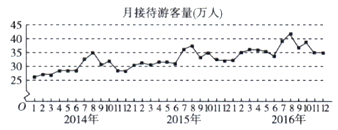
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列{an}中的项按顺序可以排成如图的形式,第一行1项,排a1;第二行2项,从左到右分别排a2,a3;第三行3项,……依此类推,设数列{an}的前n项和为Sn,则满足Sn>2019的最小正整数n的值为()

A. 20B. 21C. 26D. 27
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,长方体ABCD﹣A1B1C1D1中,AB=BC=4,BB1=2![]() ,点E、F、M分别为C1D1,A1D1,B1C1的中点,过点M的平面α与平面DEF平行,且与长方体的面相交,交线围成一个几何图形.
,点E、F、M分别为C1D1,A1D1,B1C1的中点,过点M的平面α与平面DEF平行,且与长方体的面相交,交线围成一个几何图形.
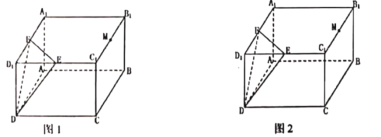
(1)在图1中,画出这个几何图形,并求这个几何图形的面积(不必说明画法与理由)
(2)在图2中,求证:D1B⊥平面DEF.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨)标准煤的几组对照数据
(吨)标准煤的几组对照数据
|
|
|
|
|
|
|
|
|
|
(1)请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司将进货单价为8元一个的商品按10元一个出售,每天可以卖出100个,若这种商品的售价每个上涨1元,则销售量就减少10个.
(1)求售价为13元时每天的销售利润;
(2)求售价定为多少元时,每天的销售利润最大,并求最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com