
【题目】对任意![]() ,
,![]() ,
,![]() ,给出下列命题:
,给出下列命题:
①“![]() ”是“
”是“![]() ”的充要条件;
”的充要条件;
②“![]() 是无理数”是“
是无理数”是“![]() 是无理数”的充要条件;
是无理数”的充要条件;
③“![]() ”是“
”是“![]() ”的必要条件,
”的必要条件,
④“![]() ”是“
”是“![]() ”的充分条件.
”的充分条件.
其中真命题的个数为().
A.1个
B.2个
C.3个
D.4个
【答案】B
【解析】
对于①,考虑![]() 时,不是必要条件,所以命题不正确;
时,不是必要条件,所以命题不正确;
对于②,根据无理数加有理数是无理数,有理数加有理数是有理数可知,命题正确;
对于③ ,小于4的数不一定小于3,但小于3的数一定小于4,说以命题正确;
对于④,![]() 时,说明不是充分条件,所以命题不正确.
时,说明不是充分条件,所以命题不正确.
对于①, ![]() ;所以“
;所以“![]() ”是“
”是“![]() ”的充分条件,
”的充分条件,
在![]() 时,
时,![]() ,此时
,此时![]() 与
与![]() 大小关系不确定,所以“
大小关系不确定,所以“![]() ”不是“
”不是“![]() ”的必要条件,故①不正确;
”的必要条件,故①不正确;
对于②,因为![]() 是无理数,5是有理数,所以
是无理数,5是有理数,所以![]() 必是无理数,所以“
必是无理数,所以“![]() 是无理数”是“
是无理数”是“![]() 是无理数”的充分条件;因为
是无理数”的充分条件;因为![]() 是无理数,5是有理数,所以
是无理数,5是有理数,所以![]() 是无理数,所以“
是无理数,所以“![]() 是无理数”是“
是无理数”是“![]() 是无理数”的必要条件,因此是充要条件,故②正确;
是无理数”的必要条件,因此是充要条件,故②正确;
对于③,因为![]() 时,必有
时,必有![]() ,所以“
,所以“![]() ”是“
”是“![]() ”的必要条件,故③正确;
”的必要条件,故③正确;
对于④,因为1>-2,但![]() ,所以 “
,所以 “![]() ”不是“
”不是“![]() ”的充分条件,故④不正确.
”的充分条件,故④不正确.
故选B.


科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点![]() 为极点,以
为极点,以![]() 轴的正半轴为极轴,且两个坐标系取相等的长度单位,已知直线
轴的正半轴为极轴,且两个坐标系取相等的长度单位,已知直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,
为参数,![]() ),曲线
),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若![]() ,求直线
,求直线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,当
两点,当![]() 变化时,求
变化时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国庆期间,某旅行社组团去风景区旅游,若旅行团人数在30人或30人以下,每人需交费用为900元;若旅行团人数多于30人,则给予优惠:每多1人,人均费用减少10元,直到达到规定人数75人为止.旅行社需支付各种费用共计15000元.
(1)写出每人需交费用![]() 关于人数
关于人数![]() 的函数;
的函数;
(2)旅行团人数为多少时,旅行社可获得最大利润?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】圆台的上、下底面半径分别为![]() 、
、![]() ,母线长
,母线长![]() ,从圆台母线
,从圆台母线![]() 的中点
的中点![]() 拉一条绳子绕圆台侧面转到
拉一条绳子绕圆台侧面转到![]() 点(
点(![]() 在下底面),求:
在下底面),求:
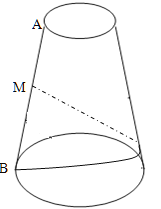
(1)绳子的最短长度;
(2)在绳子最短时,上底圆周上的点到绳子的最短距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,下列关于函数
,下列关于函数![]() 的单调性说法正确的是( )
的单调性说法正确的是( )
A.函数![]() 在
在![]() 上不具有单调性
上不具有单调性
B.当![]() 时,
时,![]() 在
在![]() 上递减
上递减
C.若![]() 的单调递减区间是
的单调递减区间是![]() ,则a的值为
,则a的值为![]()
D.若![]() 在区间
在区间![]() 上是减函数,则a的取值范围是
上是减函数,则a的取值范围是![]()
E.![]() 在区间
在区间![]() 上不可能是减函数
上不可能是减函数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在吸烟与患肺病是否相关的判断中,有下面的说法:
(1)从独立性分析可知在犯错误的概率不超过0.05的前提下,认为吸烟与患肺病有关系时,是指有![]() 的可能性使得推断错误.
的可能性使得推断错误.
(2)从独立性分析可知在犯错误的概率不超过0.01的前提下,认为吸烟与患肺病有关系时,若某人吸烟,则他有![]() 的可能患有肺病;
的可能患有肺病;
(3)若![]() ,则在犯错误的概率不超过0.01的前提下,认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;
,则在犯错误的概率不超过0.01的前提下,认为吸烟与患肺病有关系,那么在100个吸烟的人中必有99人患有肺病;
其中说法正确的是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对于函数![]() ,如果存在实数
,如果存在实数![]() 使得
使得![]() ,那么称
,那么称![]() 为
为![]() 的生成函数.
的生成函数.
(1)函数![]() ,是否为
,是否为![]() 的生成函数?说明理由;
的生成函数?说明理由;
(2)设![]() ,
,![]() ,当
,当![]() 时生成函数
时生成函数![]() ,求
,求![]() 的对称中心(不必证明);
的对称中心(不必证明);
(3)设![]() ,
,![]() ,取
,取![]() ,
,![]() ,生成函数
,生成函数![]() ,若函数
,若函数![]() 的最小值是5,求实数
的最小值是5,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 是一个由
是一个由![]() 和
和![]() 构成的
构成的![]() 行
行![]() 列的数表,且
列的数表,且![]() 中所有数字之和不小于
中所有数字之和不小于![]() ,所有这样的数表构成的集合记为
,所有这样的数表构成的集合记为![]() ,记
,记![]() 为
为![]() 的第
的第![]() 行各数之和
行各数之和![]() ,
,![]() 为
为![]() 的第
的第![]() 列各数之和
列各数之和![]() ,
,![]() 为
为![]() 、
、![]() 、
、![]() ,
,![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 中的最大值.
中的最大值.
(1)对如下数表![]() ,求
,求![]() 的值;
的值;
|
|
|
|
|
|
|
|
(2)设数表![]() ,求
,求![]() 的最小值;
的最小值;
(3)已知![]() 为正整数,对于所有的
为正整数,对于所有的![]() ,
,![]() ,且
,且![]() 的任意两行中最多有
的任意两行中最多有![]() 列各数之和为
列各数之和为![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com