练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在四棱锥中，是边长为的正三角形，为棱的中点.

    (Ⅰ)求证：平面；

    (Ⅱ)若平面平面，，求二面角的余弦值.

    【答案】(Ⅰ)见解析(Ⅱ) 二面角的余弦值为.

    【解析】

    试题分析：(Ⅰ)由面面平行判定定理证明平面//平面即可；(Ⅱ)先证平面，且，连接，分别取所在直线为轴建立空间直角坐标系，求出相关点坐及平面的法向量，平面的法向量，利用向量夹角公式可求二面角的余弦值.

    试题解析：(Ⅰ)取中点，连接，∴，∵面，面，∴面，∴平面//平面，∵平面，∴平面.

    （Ⅱ）∵，∵平面⊥平面，交线为，∴平面，且，连接，分别取所在直线为轴建立空间直角坐标系，如图所示，则点，设平面的法向量为，则，∴，即，设平面的法向量为， ，∴，因此所求二面角的余弦值为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中．

    （1）求函数的单调区间；

    （2）若函数存在两个极值点，，且，证明：．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某厂推出品牌为“玉兔”的新产品，生产“玉兔”的固定成本为20000元，每生产一件“玉兔”需要增加投入100元，根据统计数据，总收益P（单位：元）与月产量x（单位：件）满足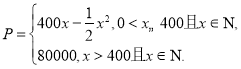（注：总收益=总成本+利润）

    （1）请将利润y（单位：元）表示成关于月产量x（单位：件）的函数；

    （2）当月产量为多少时，利润最大？最大利润是多少？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，讨论函数的单调性；

    （2）若不等式对于任意成立，求正实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为迎接2022年北京冬奥会，推广滑雪运动，某滑雪场开展滑雪促销活动．该滑雪场的收费标准是：滑雪时间不超过1小时免费，超过1小时的部分每小时收费标准为40元(不足1小时的部分按1小时计算)．有甲、乙两人相互独立地来该滑雪场运动，设甲、乙不超过1小时离开的概率分别为，；1小时以上且不超过2小时离开的概率分别为，；两人滑雪时间都不会超过3小时．

    (1)求甲、乙两人所付滑雪费用相同的概率；

    (2)设甲、乙两人所付的滑雪费用之和为随机变量ξ，求ξ的分布列与数学期望E(ξ)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】对任意，，，给出下列命题：

    ①“”是“”的充要条件；

    ②“是无理数”是“是无理数”的充要条件；

    ③“”是“”的必要条件，

    ④“”是“”的充分条件．

    其中真命题的个数为（）．

    A.1个

    B.2个

    C.3个

    D.4个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列关于回归分析与独立性检验的说法正确的是（）

    A.回归分析和独立性检验没有什么区别；

    B.回归分析是对两个变量准确关系的分析，而独立性检验是分析两个变量之间的不确定性关系；

    C.独立性检验可以确定两个变量之间是否具有某种关系．

    D.回归分析研究两个变量之间的相关关系，独立性检验是对两个变量是否具有某种关系的一种检验；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，其中无理数.

    （Ⅰ）若函数有两个极值点，求的取值范围；

    （Ⅱ）若函数的极值点有三个，最小的记为，最大的记为，若的最大值为，求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，，其中.

    （1）当时，求的单调区间；

    （2）若存在，使得不等式成立，求的取值范围.

    查看答案和解析>>

    同步练习册答案