
已知函数f(x)=(x2-3x+3)ex定义域为[-2,t](t>-2),设f(-2)=m,f(t )=n.
)=n.
(1)试确定t的取值范围,使得函数f(x)在[-2,t]上为单调函数;(2)求证:n>m;(3)若t为自然数,则当t取哪些值时,方程f(x)-m=0(m∈R)在[-2,t]上有三个不相等的实数根,并求出相应的实数m的取值范围.
(1)解:因为f′(x)=(x2-3x+3)·ex+(2x-3)·ex=x(x-1)·ex. 由f′(x)>0Þx>1或x< 0; 由f′(x)<0Þ0<x<1
0; 由f′(x)<0Þ0<x<1
所以f(x)在(-∞,0),(1,+∞)上递增,在(0,1)上递减 欲使f(x)在[-2,t]上为单调函数,则-2<t≤0. (2)证明:因为f(x)在 (-∞,0),(1,+∞)上递增,在(0,1)上递减,
(-∞,0),(1,+∞)上递增,在(0,1)上递减,
所以f(x)在x=1处取得极小值f(1)=e. 又∵f(-2)=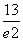 <e,所以f(x)仅在x=-2处取得[-2,t]上的最小值f(-2). 从而当t>-2时,f(-2)<f(t),即m<n.
<e,所以f(x)仅在x=-2处取得[-2,t]上的最小值f(-2). 从而当t>-2时,f(-2)<f(t),即m<n.
(3)解:由(1)知f(x)在(-∞,0),(1,+∞)上递增,在(0,1)上递减,故当t=0或t=1时,方程f(x)-m=0在[-2,t]不可能有三个不等实根,所以t≥2且t∈N.当t≥2且t∈N时,方程f(x)-m=0在[-2,t]上有三个不等实根,只需满足m∈(max(f(-2),
f(1)),min(f(0),f(t))),即可. ∴,f(0)=3,f(1)=e,f(2)=e2 ,且f(t)≥f(2)=e2>3=f(0),
,且f(t)≥f(2)=e2>3=f(0),
因而f(-2)<f(1)<f(0)<f(2)≤f(t),∴f(1)<m<f(0),即e<m<3.即实数m的取值范围是(e,3)


科目:高中数学 来源: 题型:
设函数f(x)的定义域为R,若存在与x无关的正常数M,使|f(x)|≤M|x|对一切实数x恒成立,则称f(x)为有界泛函.有下面四个函数:
①f(x)=1; ②f(x)=x2; ③f(x)=2xsinx; ④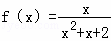 .其中属于有界泛函的是( )
.其中属于有界泛函的是( )
|
| A. | ①② | B. | ③④ | C. | ①③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:
定义域为D的函数f(x)同时满足条件①常数a,b满足a<b,区间[a,b]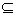 D,②使f(x)在[a,b]上的值域为[ka,kb](k∈N+),那么我们把f(x)叫做[a,b]上的“k级矩阵”函数,函数f(x)=x3是[a,b]上的“1级矩阵”函数,则满足条件的常数对(a,b)共有 ( )A.1对 B.2对 C.3对 D.4对
D,②使f(x)在[a,b]上的值域为[ka,kb](k∈N+),那么我们把f(x)叫做[a,b]上的“k级矩阵”函数,函数f(x)=x3是[a,b]上的“1级矩阵”函数,则满足条件的常数对(a,b)共有 ( )A.1对 B.2对 C.3对 D.4对
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数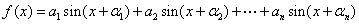 ,其中
,其中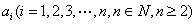 为已知实数,
为已知实数,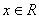 ,则下列各命题中错误的是…( )
,则下列各命题中错误的是…( )
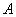 .若
.若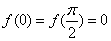 ,则
,则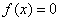 对任意实数恒成立;
对任意实数恒成立; 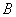 .若
.若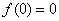 ,则函数
,则函数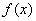 为奇函数;
为奇函数; 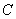 .若
.若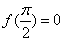 ,则函数
,则函数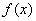 为偶函数;
为偶函数; 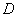 .当
.当 时,若
时,若 ,则
,则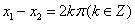
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com