
【题目】已知函数![]() ,且函数
,且函数![]() 为偶函数。
为偶函数。
(1)求![]() 的解析式;
的解析式;
(2)若方程![]() 有三个不同的实数根,求实数m的取值范围。
有三个不同的实数根,求实数m的取值范围。
科目:高中数学 来源: 题型:
【题目】某工厂拟建一座平面图(如右图所示)为矩形且面积为200平方米的三级污水处理池,由于地形限制,长、宽都不能超过16米,如果池外周壁建造单价为每米400元,中间两条隔墙建造单价为每米248元,池底建造单价为每平方米80元(池壁厚度忽略不计,且池无盖).

(1)写出总造价y(元)与污水处理池长x(米)的函数关系式,并指出其定义域;
(2)求污水处理池的长和宽各为多少时,污水处理池的总造价最低?并求最低总造价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】双曲线![]() 与椭圆
与椭圆![]() 有相同的焦点,直线
有相同的焦点,直线![]() 为双曲线
为双曲线![]() 的一条渐近线.
的一条渐近线.
(1)求双曲线![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 交双曲线
交双曲线![]() 于
于![]() 、
、![]() 两点,交
两点,交![]() 轴于
轴于![]() 点(
点(![]() 点与
点与![]() 的顶点不重合),当
的顶点不重合),当![]() ,且
,且![]() ,求
,求![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知以![]() 为首项的数列
为首项的数列![]() 满足:
满足: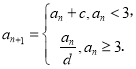
(1)当![]() ,
,![]() 时,求数列
时,求数列![]() 的通项公式;
的通项公式;
(2)当![]() ,
,![]() 时,试用
时,试用![]() 表示数列
表示数列![]() 前100项的和
前100项的和![]() ;
;
(3)当![]() (
(![]() 是正整数),
是正整数),![]() ,正整数
,正整数![]() 时,判断数列
时,判断数列![]() ,
,![]() ,
,![]() ,
,![]() 是否成等比数列?并说明理由.
是否成等比数列?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数集![]() 由实数构成,且满足:若
由实数构成,且满足:若![]() (
(![]() 且
且![]() ),则
),则![]() .
.
(1)若![]() ,试证明
,试证明![]() 中还有另外两个元素;
中还有另外两个元素;
(2)集合![]() 是否为双元素集合,并说明理由;
是否为双元素集合,并说明理由;
(3)若![]() 中元素个数不超过8个,所有元素的和为
中元素个数不超过8个,所有元素的和为![]() ,且
,且![]() 中有一个元素的平方等于所有元素的积,求集合
中有一个元素的平方等于所有元素的积,求集合![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校共有教职工900人,分成三个批次进行继续教育培训,在三个批次中男、女教职工人数如下表所示.已知在全体教职工中随机抽取一名,抽到第二批次中女职工的概率是0.16.
第一批次 | 第二批次 | 第三批次 | |
女教职工 | 196 |
|
|
男教职工 | 204 | 156 |
|
(1)求![]() 的值;
的值;
(2)现用分层抽样的方法在全体教职工中抽取54名做培训效果的调查,问应在第三批次中抽取教职工多少名?
(3)已知![]() ,
,![]() ,求第三批次中女教职工比男教职工多的概率.
,求第三批次中女教职工比男教职工多的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com