
【题目】某工厂拟建一座平面图(如右图所示)为矩形且面积为200平方米的三级污水处理池,由于地形限制,长、宽都不能超过16米,如果池外周壁建造单价为每米400元,中间两条隔墙建造单价为每米248元,池底建造单价为每平方米80元(池壁厚度忽略不计,且池无盖).

(1)写出总造价y(元)与污水处理池长x(米)的函数关系式,并指出其定义域;
(2)求污水处理池的长和宽各为多少时,污水处理池的总造价最低?并求最低总造价.
科目:高中数学 来源: 题型:
【题目】我们在求高次方程或超越方程的近似解时常用二分法求解,在实际生活中还有三分法.比如借助天平鉴别假币.有三枚形状大小完全相同的硬币,其中有一假币(质量较轻),把两枚硬币放在天平的两端,若天平平衡,则剩余一枚为假币,若天平不平衡,较轻的一端放的硬币为假币.现有 27 枚这样的硬币,其中有一枚是假币(质量较轻),如果只有一台天平,则一定能找到这枚假币所需要使用天平的最少次数为( )
A.2B.3C.4D.5
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若![]() 为偶函数,求
为偶函数,求![]() 的值并写出
的值并写出![]() 的增区间;
的增区间;
(Ⅱ)若关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,当
,当![]() 时,求
时,求![]() 的最小值;
的最小值;
(Ⅲ)对任意的![]() ,
,![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
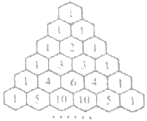
【题目】如图所示,在“杨辉三角”中,去除所有为1的项,依次构成数列2,3,3,4,6,4,5,10,10,5,…,则此数列前21项的和为_______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某温室大棚规定,一天中,从中午12点到第二天上午8点为保温时段,其余4小时为工作作业时段,从中午12点连续测量20小时,得出此温室大棚的温度y(单位:度)与时间t(单位:小时,![]() )近似地满足函数
)近似地满足函数![]() 关系,其中,b为大棚内一天中保温时段的通风量。
关系,其中,b为大棚内一天中保温时段的通风量。
(1)若一天中保温时段的通风量保持100个单位不变,求大棚一天中保温时段的最低温度(精确到0.1℃);
(2)若要保持一天中保温时段的最低温度不小于17℃,求大棚一天中保温时段通风量的最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com