
 如图,矩形CDEF所在的平面与直角梯形ABCD所在的平面垂直,其中AB∥CD,AB=1,BC=$\frac{1}{2}CD=2$,BC⊥CD,MB∥FC,MB=FC=3.P、Q分别为BC、AE的中点.
如图,矩形CDEF所在的平面与直角梯形ABCD所在的平面垂直,其中AB∥CD,AB=1,BC=$\frac{1}{2}CD=2$,BC⊥CD,MB∥FC,MB=FC=3.P、Q分别为BC、AE的中点.分析 (1)由题意可知BC⊥CD,CF⊥CD,以C为原点,分别以CD、CB、CF所在直线为x、y、z轴建立空间直角坐标系,求出所用点的坐标,得到$\overrightarrow{PQ}$的坐标,再求得平面MAB的一个法向量,由向量数量积为0得答案;
(2)分别求出两个平面AEC、ECD的法向量,然后利用法向量所成角与二面角的关系得答案.
解答  (1)证明:∵BC⊥CD,CF⊥CD,
(1)证明:∵BC⊥CD,CF⊥CD,
∴以C为原点,分别以CD、CB、CF所在直线为x、y、z轴建立空间直角坐标系,
则A(1,2,0),C(0,0,0),D(4,0,0),E(4,0,3),Q($\frac{5}{2},1,\frac{3}{2}$),P(0,1,0),
M(0,2,3),B(0,2,0),
∴$\overrightarrow{PQ}=(\frac{5}{2},0,\frac{3}{2})$,由图可得平面MAB的一个法向量$\overrightarrow{{n}_{1}}=(0,1,0)$,
∵$\overrightarrow{PQ}•\overrightarrow{{n}_{1}}=(\frac{5}{2},0,\frac{3}{2})•(0,1,0)=0$,
∴$\overrightarrow{PQ}⊥\overrightarrow{{n}_{1}}$,又PQ?面MAB,
∴PQ∥平面MAB;
(2)解:设平面AEC的一个法向量为$\overrightarrow{{n}_{2}}=({x}_{2},{y}_{2},{z}_{2})$,平面ECD的一个法向量为$\overrightarrow{{n}_{3}}=({x}_{3},{y}_{3},{z}_{3})$,
∴$\left\{\begin{array}{l}{\overrightarrow{{n}_{2}}•\overrightarrow{AE}=0}\\{\overrightarrow{{n}_{2}}•\overrightarrow{AC}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{3{x}_{2}-2{y}_{2}+3{z}_{2}=0}\\{-{x}_{2}-2{y}_{2}=0}\end{array}\right.$,则$\overrightarrow{{n}_{2}}=(2,-1,-\frac{8}{3})$;
$\left\{\begin{array}{l}{\overrightarrow{{n}_{3}}•\overrightarrow{EC}=0}\\{\overrightarrow{{n}_{3}}•\overrightarrow{ED}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{-4{x}_{3}-3{z}_{3}=0}\\{-3{z}_{3}=0}\end{array}\right.$,则$\overrightarrow{{n}_{3}}=(0,1,0)$.
设二面角A-EC-D的平面角为θ,
则cosθ=|cos<$\overrightarrow{{n}_{2}},\overrightarrow{{n}_{3}}$>|=$\frac{|\overrightarrow{{n}_{2}}•\overrightarrow{{n}_{3}}|}{|\overrightarrow{{n}_{2}}|•|\overrightarrow{{n}_{3}}|}$=$\frac{1}{\sqrt{1}•\sqrt{\frac{109}{9}}}=\frac{3\sqrt{109}}{109}$.
点评 本题主要考查直线与平面之间的平行、垂直等位置关系,二面角的概念、求法等知识,以及空间想象能力和逻辑推理能力,是中档题.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:解答题
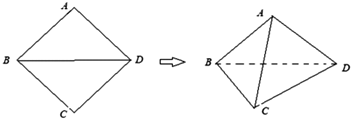
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知直三棱柱底面各边的比为17:10:9,侧棱长为16cm,全面积为1440cm2,求底面各边之长.(提示:设△ABC的三边长分别为a,b,c,记p=$\frac{1}{2}$(a+b+c),则△ABC的面积S△ABC=$\sqrt{p(p-a)(p-b)(p-c)}$.
已知直三棱柱底面各边的比为17:10:9,侧棱长为16cm,全面积为1440cm2,求底面各边之长.(提示:设△ABC的三边长分别为a,b,c,记p=$\frac{1}{2}$(a+b+c),则△ABC的面积S△ABC=$\sqrt{p(p-a)(p-b)(p-c)}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
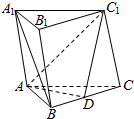 如图,正三棱柱ABC-A1B1C1的各棱均相等,AB=2,D是BC上的一点,AD⊥C1D.
如图,正三棱柱ABC-A1B1C1的各棱均相等,AB=2,D是BC上的一点,AD⊥C1D.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
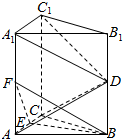 在直三棱柱ABC-A1B1C1中,D、E、F分别是BB1、AA1、AC的中点,AC=BC=$\frac{1}{2}$AA1,AB=$\sqrt{2}$AC
在直三棱柱ABC-A1B1C1中,D、E、F分别是BB1、AA1、AC的中点,AC=BC=$\frac{1}{2}$AA1,AB=$\sqrt{2}$AC查看答案和解析>>
科目:高中数学 来源: 题型:解答题
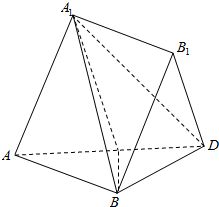 如图,多面体A1B1-ABC中,△ABC与△AA1C都是边长为2的正三角形,四边形ABB1A1是平行四边形,且平面A1AC⊥平面ABC.
如图,多面体A1B1-ABC中,△ABC与△AA1C都是边长为2的正三角形,四边形ABB1A1是平行四边形,且平面A1AC⊥平面ABC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com