
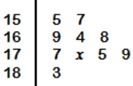
 在某个班随机抽取了10名学生的身高数据如下茎叶图所示(单位:cm),且该组数据的中位数为171,茎叶图中有一个数据被污损,用字母x表示.
在某个班随机抽取了10名学生的身高数据如下茎叶图所示(单位:cm),且该组数据的中位数为171,茎叶图中有一个数据被污损,用字母x表示.分析 (1)根据该组数据的中位数为171,求x的值,从而估计该班学生身高的平均值;
(2)列举基本事件,利用古典概型概率公式求解即可.
解答 解:(1)把这10个数据按从小到大排列后,位于中间的两个数据中的其中一个为169,另一个为175或者170+x,又因为该组数据的中位数为171,
所以$\frac{175+169}{2}=171$(舍去)或$\frac{{({170+x})+169}}{2}=171$,解之得x=3;
平均值为$\frac{155+157+169+164+168+177+173+175+179+183}{10}=170({cm})$;
(2)所有可能的结果列举如下:(177,173,175),(177,173,179),(177,173,183),(177,175,179),(177,175,183),(177,179,183),(173,175,179),(173,175,183),(173,179,183),(175,179,183),共10种,
其中,至少有两名学生的身高低于178cm的结果列举如下,(177,173,175),(177,173,179),(177,173,183),(177,175,179),(177,175,183),(173,175,179),(173,175,183),共7种,
至少有两名学生的身高低于178cm的概率为$\frac{7}{10}$.
点评 本题考查茎叶图,列举出计算基本事件及事件发生的概率,难度不大,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3+\sqrt{5}}}{2}$ | B. | $\sqrt{\frac{{\sqrt{5}+1}}{2}}$ | C. | $\frac{{\sqrt{5}-1}}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1.2] | B. | (1.2] | C. | [1.2) | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com