
分析 (1)由直线l过点A(1,2),且倾斜角$\frac{π}{4}$,可得直线l的参数方程为$\left\{\begin{array}{l}{x=1+tcos\frac{π}{4}}\\{y=2+tsin\frac{π}{4}}\end{array}\right.$(t为参数).由圆C的极坐标方程为ρ2=2ρcosθ,利用互化公式可得:圆C的直角坐标方程.
(2)求出圆心到直线的距离d,与半径比较即可得出.
解答 解:(1)∵直线l过点A(1,2),且倾斜角$\frac{π}{4}$,∴直线l的参数方程为 $\left\{{\begin{array}{l}{x=1+\frac{{\sqrt{2}}}{2}t}\\{y=2+\frac{{\sqrt{2}}}{2}t}\end{array}}\right.$(t为参数).
∵圆C的极坐标方程为ρ2=2ρcosθ,∴圆C的直角坐标方程为x2+y2=2x,即(x-1)2+y2=1.
(2)直线l的普通方程为y-x-1=0,圆心C(1,0)到直线l的距离$d=\frac{2}{{\sqrt{2}}}=\sqrt{2}>1$,
∴直线l与圆C相离.
点评 本题考查了参数方程化为普通方程、极坐标方程化为直角坐标方程、点到直线的距离公式、直线与圆的位置关系,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | -1 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 日销售量 | 1 | 1.5 | 2 |
| 天数 | 10 | 25 | 15 |
| 频率 | 0.2 | a | b |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
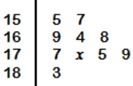 在某个班随机抽取了10名学生的身高数据如下茎叶图所示(单位:cm),且该组数据的中位数为171,茎叶图中有一个数据被污损,用字母x表示.
在某个班随机抽取了10名学生的身高数据如下茎叶图所示(单位:cm),且该组数据的中位数为171,茎叶图中有一个数据被污损,用字母x表示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=\frac{{{x^2}-1}}{x-1}$与g(x)=x+1 | B. | f(x)=x与$g(x)={(\sqrt{x})^2}$ | ||
| C. | $f(x)=\sqrt{x^2}$与g(x)=x | D. | f(x)=x2-2x+1与g(t)=(t-1)2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥n,m⊥α,则α⊥β | B. | 若α∥β,m⊥n,则m⊥α | C. | 若α∥β,m?α,则m∥n | D. | 若m∥n,m?α,则α∥β |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com