
分析 已知直线l过点M(1,2),点M在圆内,$sin\frac{1}{2}∠ACB=\frac{{\frac{1}{2}|AB|}}{r}=\frac{|AB|}{2r}$,因此要使∠ACB最小,则|AB|取最小值.
解答 解:由已知直线l过点M(1,2),点M在圆内,
∵$sin\frac{1}{2}∠ACB=\frac{{\frac{1}{2}|AB|}}{r}=\frac{|AB|}{2r}$,因此要使∠ACB最小,则|AB|取最小值,
又AB过点M,因此M为AB中点,即CM⊥AB,
因为${k_{CM}}=\frac{4-2}{3-1}=1$,所以kl=-1,
所以l的方程为y-2=-(x-1),即x+y-3=0.
点评 本题主要考查了直线与圆的基础知识点,以及斜率与直线关系,属中档题.


科目:高中数学 来源: 题型:选择题
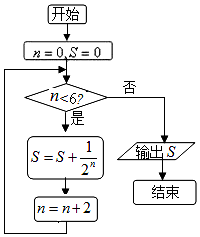
| A. | $\frac{5}{4}$ | B. | $\frac{21}{16}$ | C. | $\frac{63}{32}$ | D. | $\frac{85}{64}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3+\sqrt{5}}}{2}$ | B. | $\sqrt{\frac{{\sqrt{5}+1}}{2}}$ | C. | $\frac{{\sqrt{5}-1}}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com