
如图所示的两个同心圆盘均被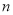 等分(
等分( 且
且 ),在相重叠的扇形格中依次同时填上
),在相重叠的扇形格中依次同时填上 ,内圆盘可绕圆心旋转,每次可旋转一个扇形格,当内圆盘旋转到某一位置时,定义所有重叠扇形格中两数之积的和为此位置的“旋转和”.
,内圆盘可绕圆心旋转,每次可旋转一个扇形格,当内圆盘旋转到某一位置时,定义所有重叠扇形格中两数之积的和为此位置的“旋转和”.
(1)求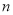 个不同位置的“旋转和”的和;
个不同位置的“旋转和”的和;
(2)当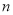 为偶数时,求
为偶数时,求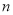 个不同位置的“旋转和”的最小值;
个不同位置的“旋转和”的最小值;
(3)设 ,在如图所示的初始位置将任意
,在如图所示的初始位置将任意 对重叠的扇形格中的两数均改写为0,证明:当
对重叠的扇形格中的两数均改写为0,证明:当 时,通过旋转,总存在一个位置,任意重叠的扇形格中两数不同时为0.
时,通过旋转,总存在一个位置,任意重叠的扇形格中两数不同时为0.

(1)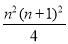 ;(2) 最小值
;(2) 最小值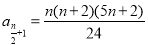 ;(3)详见解析.
;(3)详见解析.
【解析】
试题分析:(1)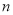 个不同位置的“旋转和”的和,就是将所有位置的旋转相加,故内盘中的任一数都会和外盘中的每个数作积;(2)设内盘中的
个不同位置的“旋转和”的和,就是将所有位置的旋转相加,故内盘中的任一数都会和外盘中的每个数作积;(2)设内盘中的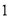 和外盘中的
和外盘中的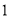 同扇形格时的“旋转和”为
同扇形格时的“旋转和”为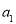 ;设内盘中的
;设内盘中的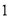 和外盘中的
和外盘中的 同扇形格时的“旋转和”为
同扇形格时的“旋转和”为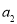 ;依次下去,设内盘中的
;依次下去,设内盘中的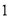 和外盘中的
和外盘中的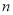 同扇形格时的“旋转和”为
同扇形格时的“旋转和”为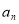 ;这样便得一个数列.这样问题转化为求该数列的最小值.求数列的最值,首先研究数列的单调性,而研究数列的单调性,就是研究相邻两项的差的符号,即研究
;这样便得一个数列.这样问题转化为求该数列的最小值.求数列的最值,首先研究数列的单调性,而研究数列的单调性,就是研究相邻两项的差的符号,即研究 的符号;(3)显然直接证明有点困难,故采用反证法.由于该问题只涉及0与非0的问题,故可将图中所有非
的符号;(3)显然直接证明有点困难,故采用反证法.由于该问题只涉及0与非0的问题,故可将图中所有非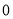 数改写为
数改写为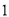 ,这样共有
,这样共有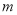 个0,
个0,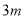 个1.假设任意位置,总存在一个重叠的扇形格中两数同时为
个1.假设任意位置,总存在一个重叠的扇形格中两数同时为 ,则此位置的“旋转和”必大于或等于
,则此位置的“旋转和”必大于或等于 ,初始位置外的
,初始位置外的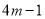 个位置的“旋转和”的和为
个位置的“旋转和”的和为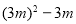 ,则有
,则有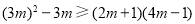 ,即
,即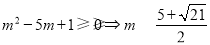 ,这与
,这与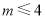 矛盾,故命题得证.
矛盾,故命题得证.
试题解析:(1)由于内盘中的任一数都会和外盘中的每个作积,故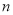 个不同位置的“旋转和”的和为
个不同位置的“旋转和”的和为
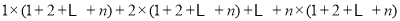
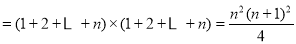 ; 3分
; 3分
(2)设内盘中的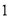 和外盘中的
和外盘中的 同扇形格时的“旋转和”为
同扇形格时的“旋转和”为
则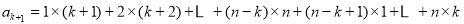

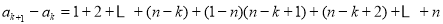
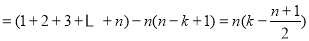 5分
5分
所以当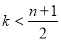 时,
时,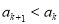 ,当
,当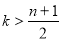 时,
时,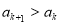 ,所以
,所以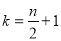 时,
时,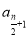 最小
最小
最小值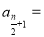

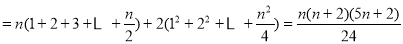 ; 8分
; 8分
(3)证明:将图中所有非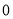 数改写为
数改写为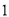 ,现假设任意位置,总存在一个重叠的扇形格中两数同时为
,现假设任意位置,总存在一个重叠的扇形格中两数同时为 ,则此位置的“旋转和”必大于或等于
,则此位置的“旋转和”必大于或等于 ,初始位置外的
,初始位置外的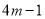 个位置的“旋转和”的和为
个位置的“旋转和”的和为
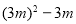 ,则有
,则有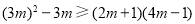 ,即
,即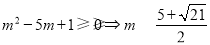 ,这与
,这与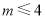 矛盾,故命题得证. 12分
矛盾,故命题得证. 12分
考点:数列及数列的和.


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:高中数学 来源:2013-2014学年陕西省高考第七次适应性训练文科数学试卷(解析版) 题型:选择题
已知 的三顶点坐标为
的三顶点坐标为 ,
, ,
, ,
, 点的坐标为
点的坐标为 ,向
,向 内部投一点
内部投一点 ,那么点
,那么点 落在
落在 内的概率为( ).
内的概率为( ).
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西省高三第六次模拟理科数学试卷(解析版) 题型:选择题
已知O, A, M,B为平面上四点,且 ,实数
,实数 ,则
,则
A. 点M在线段AB上 B. 点B在线段AM上
C. 点A在线段BM上 D. O,A,M,B一定共线
查看答案和解析>>
科目:高中数学 来源:2013-2014学年陕西省高三第六次模拟文科数学试卷(解析版) 题型:选择题
在A,B两个袋中都有6张分别写有数字0,1,2,3,4, 5的卡片,现
从每个袋中任取一张卡片,则两张卡片上数字之和为7的概率为
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年重庆市高三下学期考前模拟(二诊)理科数学试卷(解析版) 题型:解答题
已知向量 ,函数
,函数 的最小正周期为
的最小正周期为 .
.
(1)求 的值;
的值;
(2)设 的三边
的三边 、
、 、
、 满足:
满足: ,且边
,且边 所对的角为
所对的角为 ,若关于
,若关于 的方程
的方程 有两个不同的实数解,求实数
有两个不同的实数解,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年重庆市高三下学期考前模拟(二诊)理科数学试卷(解析版) 题型:选择题
已知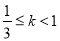 ,函数
,函数 的零点分别为
的零点分别为 ,函数
,函数 的零点分别为
的零点分别为 ,则
,则 的最小值为( )
的最小值为( )
(A)1 (B) (C)
(C) (D)3
(D)3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com