
如图,已知正四棱锥P-ABCD的所有棱长都是2,底面正方形两条对角线相交于O点,M是侧棱PC的中点.
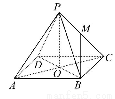
(1)求此正四棱锥的体积.
(2)求直线BM与侧面PAB所成角θ的正弦值.
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十四第七章第三节练习卷(解析版) 题型:填空题
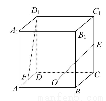
如图,在棱长为2的正方体ABCD -A1B1C1D1中,点O是底面ABCD的中心,点E,F分别是CC1,AD的中点,则异面直线OE与FD1所成角的余弦值为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十五第七章第四节练习卷(解析版) 题型:解答题
如图所示,四边形EFGH所在平面为三棱锥A-BCD的一个截面,四边形EFGH为平行四边形.
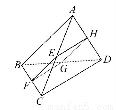
(1)求证:AB∥平面EFGH,CD∥平面EFGH.
(2)若AB=4,CD=6,求四边形EFGH周长的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十二第七章第一节练习卷(解析版) 题型:解答题
用一个平行于圆锥底面的平面截这个圆锥,截得圆台上、下底面的面积之比为1∶16,截去的圆锥的母线长是3cm,求圆台的母线长.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十二第七章第一节练习卷(解析版) 题型:选择题
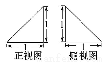
一个锥体的正视图和侧视图如图所示,下面选项中,不可能是该锥体的俯视图的是( )
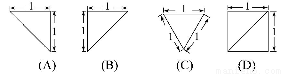
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十九第七章第八节练习卷(解析版) 题型:选择题
如图,平面ABCD⊥平面ABEF,四边形ABCD是正方形,四边形ABEF是矩形,且AF= AD=a,G是EF的中点,则GB与平面AGC所成角的正弦值为( )
AD=a,G是EF的中点,则GB与平面AGC所成角的正弦值为( )
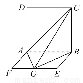
(A) (B)
(B)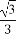 (C)
(C)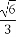 (D)
(D)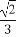
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十七第七章第六节练习卷(解析版) 题型:解答题
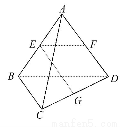
如图所示,已知空间四边形ABCD的每条边和对角线长都等于1,点E,F,G分别是AB,AD,CD的中点,计算:
(1)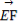 ·
·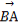 .
.
(2)EG的长.
(3)异面直线EG与AC所成角的大小.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业四十 第六章第六节练习卷(解析版) 题型:选择题
若|loga |=loga
|=loga ,|logba|=-logba,则a,b满足的条件是( )
,|logba|=-logba,则a,b满足的条件是( )
(A)a>1,b>1 (B)0<a<1,b>1
(C)a>1,0<b<1 (D)0<a<1,0<b<1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com