
| 1 |
| 2 |
| n+1 |
| n |
| 5n |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2 |
| n |
| 2n |
| n+1 |
| n |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| n+5 |
| 2n+1 |
| n+5 |
| 2n |
| n+5 |
| 2n |
| 5n |
| 2n+1 |
| 15 |
| 7 |
| k+5 |
| 2k |
| 5k |
| 2k+1 |
| k+6 |
| 2k+1 |
| 5k |
| 2k+1 |
| k+5 |
| 2k |
| k+6 |
| 2k+1 |
| 5(k+1) |
| 2k+3 |
| 5n |
| 2n+1 |


科目:高中数学 来源: 题型:
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| 16 |
| 5 |
| 11π |
| 6 |
| 20 |
| 13 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 4 |
| a2n-1a2n+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
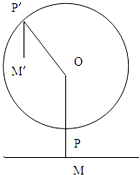 六一儿重节到了,小明与爸爸去游乐场看见了大观览车,已知大观览车轮轴中心为点O,距地面高为32m(即OM=32m),巨轮半径为30m,点p为吊舱与轮的连接点,吊舱高2m(即PM=2m)巨轮每分钟转动30°,小明和爸爸从地面M点进入吊舱后,巨轮开始逆时针转动.
六一儿重节到了,小明与爸爸去游乐场看见了大观览车,已知大观览车轮轴中心为点O,距地面高为32m(即OM=32m),巨轮半径为30m,点p为吊舱与轮的连接点,吊舱高2m(即PM=2m)巨轮每分钟转动30°,小明和爸爸从地面M点进入吊舱后,巨轮开始逆时针转动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com