
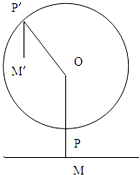
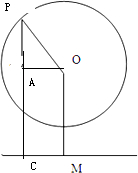
 六一儿重节到了,小明与爸爸去游乐场看见了大观览车,已知大观览车轮轴中心为点O,距地面高为32m(即OM=32m),巨轮半径为30m,点p为吊舱与轮的连接点,吊舱高2m(即PM=2m)巨轮每分钟转动30°,小明和爸爸从地面M点进入吊舱后,巨轮开始逆时针转动.
六一儿重节到了,小明与爸爸去游乐场看见了大观览车,已知大观览车轮轴中心为点O,距地面高为32m(即OM=32m),巨轮半径为30m,点p为吊舱与轮的连接点,吊舱高2m(即PM=2m)巨轮每分钟转动30°,小明和爸爸从地面M点进入吊舱后,巨轮开始逆时针转动.| π |
| 6 |
| 2π |
| ω |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
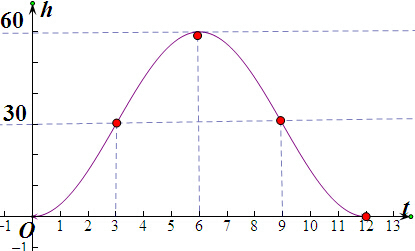
| t | 0 | 3 | 6 | 9 | 12 | ||||||
| 0 |
| π |
| 2π | ||||||
| h | 0 | 30 | 60 | 30 | 0 |


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
| n+1 |
| n |
| 5n |
| 2n+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 围棋社 | 舞蹈社 | 拳击社 | |
| 男生 | 5 | 10 | 28 |
| 女生 | 15 | 30 | m |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| x |
| 1 |
| 3 |
| 1 |
| 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| Sn |
| 4 |
| (an+1)(an+1+1) |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
| h(x1)-h(x2) |
| x1-x2 |
| 2 |
| 3 |
| 3 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com