
| 2 |
| 4 |
| a2n-1a2n+1 |
| 2 |
| 4 |
| a2n-1a2n+1 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 2 |
| 4 |
| a2n-1a2n+1 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 2(1-2n) |
| 1-2 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| 3n+2 |
| 2n+1 |


科目:高中数学 来源: 题型:
| (an+1)•2n-1 |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| n+1 |
| n |
| 5n |
| 2n+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 函数f(x)=6cos2
函数f(x)=6cos2| ωx |
| 2 |
| 3 |
8
| ||
| 5 |
| 10 |
| 3 |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
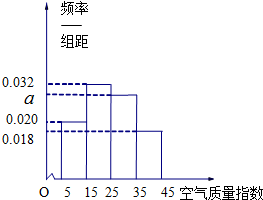 去年2月29日,我国发布了新修订的《环境空气质量标准》指出空气质量指数在0-50为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的空气质量指数频率分布直方图,如图.
去年2月29日,我国发布了新修订的《环境空气质量标准》指出空气质量指数在0-50为优秀,各类人群可正常活动.惠州市环保局对我市2014年进行为期一年的空气质量监测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为(5,15],(15,25],(25,35],(35,45],由此得到样本的空气质量指数频率分布直方图,如图.. |
| X |
查看答案和解析>>
科目:高中数学 来源: 题型:
| a |
| x |
| 1 |
| 3 |
| 1 |
| 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com