
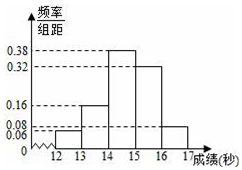
 某学校高三年级800名学生在一次百米测试中,成绩全部在12秒到17秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[12,13),第二组[13,14),…,第五组[16,17],如图是根据上述分组得到的频率分布直方图.
某学校高三年级800名学生在一次百米测试中,成绩全部在12秒到17秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[12,13),第二组[13,14),…,第五组[16,17],如图是根据上述分组得到的频率分布直方图.分析 (1)由频率分布直方图,先求出成绩小于13秒的频率,由此能求出该样本在这次百米测试中成绩优秀的人数.
(2)由频率分布直方图能估计本次测试的平均成绩.
(3)由频率分布直方图,得第一组的频率为0.06,第五组的频率为0.08,从而得到第一组有3人,第五组有4人,进而第一组中有1名女生2名男生,第五组中有3名女生1名男生,现从第一、第五组中各抽取1名学生组成一个实验组,利用列兴法能求出所抽取的2名同学中恰好为一名男生和一名女生的概率.
解答 解:(1)由频率分布直方图,得成绩小于13秒的频率为0.06,
∴该样本在这次百米测试中成绩优秀的人数为:0.06×50=3(人).┅┅┅┅3分
(2)由频率分布直方图估计本次测试的平均成绩为:
12.5×0.06+13.5×0.16+14.5×0.38+15.5×0.32+16.5×0.08=14.7┅┅┅┅┅┅┅6分
(3)由频率分布直方图,得第一组的频率为0.06,第五组的频率为0.08,
∴第一组有50×0.06=3人,第五组有50×0.08=4人,…7分
∵样本中第一组只有一名女生,第五组只有一名男生,
∴第一组中有1名女生2名男生,第五组中有3名女生1名男生,
现从第一、第五组中各抽取1名学生组成一个实验组,
设第一组中三人分别为a1,a2,a3,其中a1为女生,第五组中四人分别为b1,b2,b3,b4,其中b1为男生,
则基本时间空间为Ω={(a1,b1)(a1,b2)(a1,b3)(a1,b4)(a2,b1)(a2,b2)(a2,b3)
(a2,b4)(a3,b1)(a3,b2)(a3,b3)(a3,b4)}
n=12,┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅9分
所抽取的2名同学中恰好为一名男生和一名女生,包含的基本事件个数m=7,
∴所求概率为p=$\frac{m}{n}$=$\frac{7}{12}$.┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅12分.
点评 本题考查频率分布直方图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{10}}}{2}$ | B. | $\sqrt{10}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
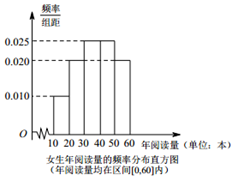 每年的4月23日为世界读书日,为调查某高校学生(学生很多)的读书情况,随机抽取了男生,女生各20人组成的一个样本,对他们的年阅读量(单位:本)进行了统计,分析得到了男生年阅读量的频数分布表和女生年阅读量的频率分布直方图.
每年的4月23日为世界读书日,为调查某高校学生(学生很多)的读书情况,随机抽取了男生,女生各20人组成的一个样本,对他们的年阅读量(单位:本)进行了统计,分析得到了男生年阅读量的频数分布表和女生年阅读量的频率分布直方图.| 本/年 | [0,10) | [10,20) | [20,30) | [30,40) | [40,50) | [50,60] |
| 频数 | 3 | 1 | 8 | 4 | 2 | 2 |
| 性别 阅读量 | 丰富 | 不丰富 | 合计 |
| 男 | |||
| 女 | |||
| 合计 |
| P(K2≥k0) | 0.025 | 0.010 | 0.005 |
| k0 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2} | B. | {-2,-1,0,1,2} | C. | {1} | D. | {0,1,2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45° | B. | 30° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({1,\sqrt{2}})$ | B. | $({1,\sqrt{3}})$ | C. | (1,2) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $\sqrt{5}$ | C. | 3 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,21-x>0 | |
| B. | ?a∈R,使函数y=xa的图象关于y轴对称 | |
| C. | ?a∈R,函数y=xa的图象经过第四象限 | |
| D. | ?x∈(0,+∞),使2x>x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com