
分析 欲求数列$\{{log_2}\frac{a_n}{n+1}\}$的前10项和,必须求出在x=2处的切线方程,须求出其斜率的值即可,故先利用导数求出在x=2处的导函数值,再结合导数的几何意义即可求出切线的斜率即得直线方程进而得到切线与y轴交点的纵坐标.最后利用对数的运算性质和等差数列的求和公式计算,从而问题解决.
解答 解:y′=nxn-1-(n+1)xn,
曲线y=xn(1-x)在x=2处的切线的斜率为k=n•2n-1-(n+1)•2n,
切点为(2,-2n),
所以切线方程为y+2n=k(x-2),
令x=0得an=(n+1)2n,
令bn=log2$\frac{{a}_{n}}{n+1}$.
数列{bn}的前10项和为log22+log222+log223+…+log2210
=1+2+3+…+10=$\frac{1}{2}$×10×11=55.
故答案为:55.
点评 本题考查应用导数求曲线切线的斜率,数列通项公式以及等差数列的前n项和的公式.解后反思:应用导数求曲线切线的斜率时,要首先判定所经过的点为切点.否则容易出错.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
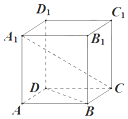 如图,四棱柱ABCD-A1B1C1D1的底面是菱形且D1D⊥平面ABCD,则A1C与BD所成的角是( )
如图,四棱柱ABCD-A1B1C1D1的底面是菱形且D1D⊥平面ABCD,则A1C与BD所成的角是( )| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
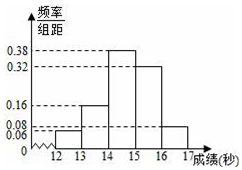 某学校高三年级800名学生在一次百米测试中,成绩全部在12秒到17秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[12,13),第二组[13,14),…,第五组[16,17],如图是根据上述分组得到的频率分布直方图.
某学校高三年级800名学生在一次百米测试中,成绩全部在12秒到17秒之间,抽取其中50个样本,将测试结果按如下方式分成五组:第一组[12,13),第二组[13,14),…,第五组[16,17],如图是根据上述分组得到的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{y^2}{3}-{x^2}=1$ | B. | $\frac{x^2}{4}-\frac{y^2}{12}=1$ | C. | ${y^2}-\frac{x^2}{3}=1$ | D. | $\frac{x^2}{12}-\frac{y^2}{4}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 0 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3∈A | B. | A∩B=(-1,0) | C. | A∪B=R | D. | A?B |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=±$\frac{\sqrt{3}}{3}$x | B. | y=±$\frac{1}{3}$x | C. | y=±$\sqrt{3}$x | D. | y=$±\frac{\sqrt{3}}{2}$x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com