
 (Ⅱ)
(Ⅱ)
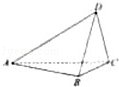
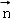 =(l,m,n)是平面ABD的法向量,由(Ⅰ)易得向量
=(l,m,n)是平面ABD的法向量,由(Ⅰ)易得向量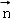 的坐标,同时易得
的坐标,同时易得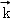 =(0,0,1)是平面ABC的法向量,由向量的夹角公式可得从而cos<
=(0,0,1)是平面ABC的法向量,由向量的夹角公式可得从而cos<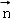 ,
,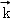 >,进而由同角三角函数的基本关系,可得tan<
>,进而由同角三角函数的基本关系,可得tan<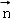 ,
,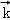 >,即可得答案.
>,即可得答案.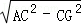 =
=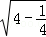 =
=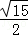 ;
;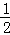 AC•DF=
AC•DF=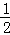 CD•AG可得,DF=
CD•AG可得,DF=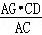 =
=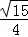 ;
;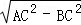 =
=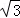 ,
, AB•BC=
AB•BC=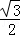 ;
;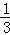 ×S△ABC×DF=
×S△ABC×DF=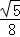 ;
;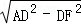 =
=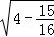 =
= ;
;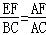 ,可得EF=
,可得EF=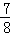 ;
;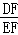 =
=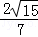 .
.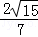 .
.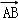 ⊥
⊥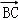 ,|
,|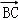 |=1;
|=1;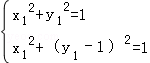 ,
,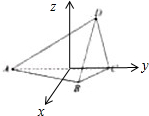
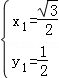 或
或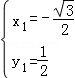 (舍);
(舍);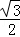 ,
, ,0),
,0),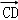 |=1,|
|=1,|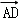 |=2,有(y2﹣1)2+z22=1且(y2+1)2+z22=1;
|=2,有(y2﹣1)2+z22=1且(y2+1)2+z22=1;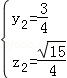 或
或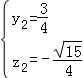 (舍),
(舍),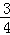 ,
,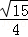 ),
),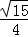
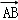 |=
|=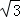 ,|
,|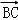 |=1;
|=1;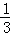 ×
×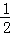 ×|
×|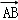 |×|
|×|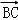 |h=
|h=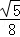 ;
;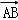 =(
=(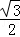 ,
,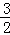 ,0),
,0),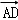 =(0,
=(0,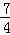 ,
,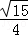 ),
),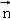 =(l,m,n)是平面ABD的法向量,则由
=(l,m,n)是平面ABD的法向量,则由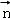 ⊥
⊥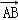 可得,
可得,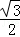 l+
l+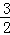 m=0,(1);
m=0,(1);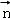 ⊥
⊥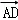 可得,
可得,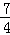 m+
m+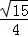 n=0,(2);
n=0,(2);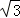 ,n=
,n=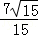 ,即
,即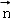 =(
=(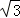 ,﹣1,
,﹣1,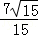 )
)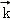 =(0,0,1)是平面ABC的法向量,
=(0,0,1)是平面ABC的法向量,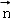 ,
,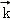 >=
>=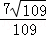 ;
;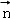 ,
,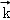 >=
>=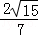 ;
;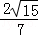 .
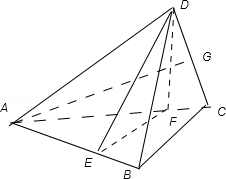
.


科目:高中数学 来源:不详 题型:解答题
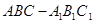 中,
中,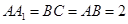 ,
,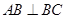 。M、N分别是AC和BB1的中点。
。M、N分别是AC和BB1的中点。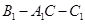 的大小。
的大小。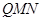 ⊥平面
⊥平面 ,
, 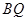 的长度。
的长度。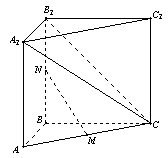
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
A.2
| B.
| C.|a+b+c| | D.2|a+b+c| |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.(-3,1,-4) | B.(3,-1,-4) | C.(-3,-1,-4) | D.(-3,,1,-4) |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
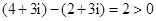 ,所以
,所以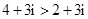 ;
;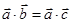 两边同除
两边同除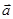 ,可得
,可得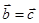 ;
; 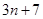 的一个通项公式是
的一个通项公式是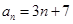 ;
; | A.1个 | B.2个 | C.3个 | D.4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com