
在单调递增数列 中,
中,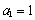 ,
, ,且
,且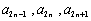 成等差数列,
成等差数列, 成等比数列,
成等比数列,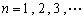 .
.
(1)分别计算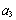 ,
,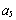 和
和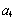 ,
,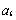 的值;
的值;
(2)求数列 的通项公式(将
的通项公式(将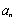 用
用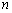 表示);
表示);
(3)设数列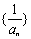 的前
的前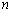 项和为
项和为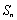 ,证明:
,证明: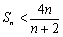 ,
,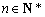 .
.
在单调递增数列 中,
中,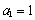 ,
, ,且
,且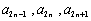 成等差数列,
成等差数列, 成等比数列,
成等比数列,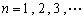 .
.
(1)分别计算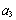 ,
,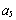 和
和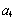 ,
,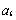 的值;
的值;
(2)求数列 的通项公式(将
的通项公式(将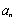 用
用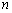 表示);
表示);
(3)设数列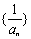 的前
的前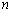 项和为
项和为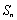 ,证明:
,证明: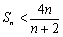 ,
,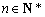 .
.
解:(1)由已知,得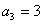 ,
,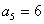 ,
,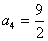 ,
,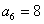 .
.
(2)(证法1)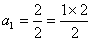 ,
,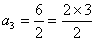 ,
,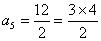 ,……;
,……;
 ,
,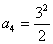 ,
,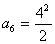 ,…….∴猜想
,…….∴猜想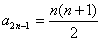 ,
,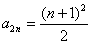 ,
,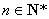 ,
,
以下用数学归纳法证明之.
①当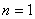 时,
时,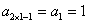 ,
, ,猜想成立;
,猜想成立;
②假设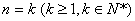 时,猜想成立,即
时,猜想成立,即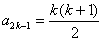 ,
,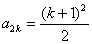 ,那么
,那么
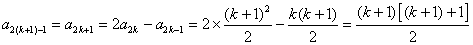
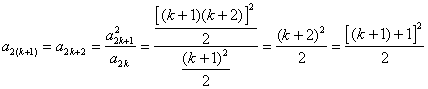
∴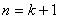 时,猜想也成立.由①②,根据数学归纳法原理,对任意的
时,猜想也成立.由①②,根据数学归纳法原理,对任意的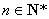 ,猜想成立.
,猜想成立.
∴当 为奇数时,
为奇数时,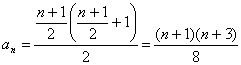 ;
;
当 为偶数时,
为偶数时,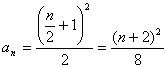 .
.
即数列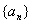 的通项公式为
的通项公式为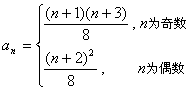 .
.
(3)(解法2)证明:
当 为奇数时,
为奇数时,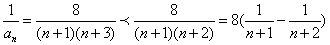
当 为偶数时,.
为偶数时,.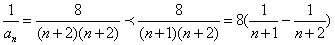
综上,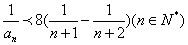
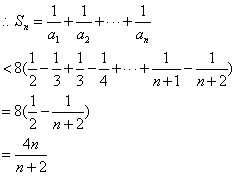
(解法2)由(2),得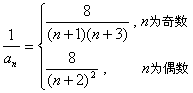 .
.
以下用数学归纳法证明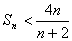 ,
,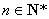 .
.
①当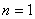 时,
时,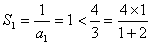 ;
;
当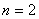 时,
时,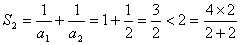 .∴
.∴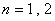 时,不等式成立.
时,不等式成立.
②假设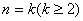 时,不等式成立,即
时,不等式成立,即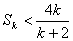 ,
,
那么,当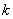 为奇数时,
为奇数时,
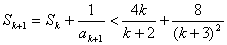
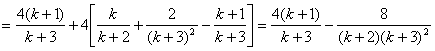
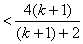 ;
;
当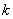 为偶数时,
为偶数时,
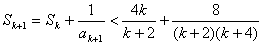
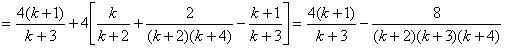
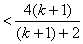 .∴
.∴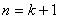 时,不等式也成立.
时,不等式也成立.
综上所述: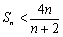


科目:高中数学 来源: 题型:
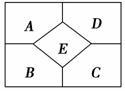
如图所示的五个区域中,中心区域是一幅图画,现要求在
其余四个区域中涂色,有四种颜色可供选择.要求每个区域只涂一种颜色,相邻区域所涂颜色不同,则不同的涂色方法种数为
A.84 B.72 C.64 D.56
 |
查看答案和解析>>
科目:高中数学 来源: 题型:
用反证法证明命题“若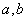 为实数,则一元二次方程
为实数,则一元二次方程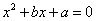 没有实根”时,要做的假设正确的是( )
没有实根”时,要做的假设正确的是( )
A.方程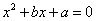 至多一个实根 B.方程
至多一个实根 B.方程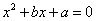 没有实根
没有实根
C.方程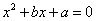 至多有两个实根 D.方程
至多有两个实根 D.方程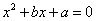 恰好有两个实根
恰好有两个实根
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com