
已知椭圆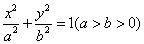 经过点
经过点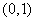 ,过右焦点F且不与x轴重合的动直线L交椭圆于
,过右焦点F且不与x轴重合的动直线L交椭圆于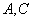 两点,当动直线L的斜率为2时,坐标原点O到L的距离为
两点,当动直线L的斜率为2时,坐标原点O到L的距离为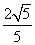 . (Ⅰ) 求椭圆的方程;
. (Ⅰ) 求椭圆的方程;
(Ⅱ) 过F的另一直线交椭圆于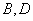 两点,且
两点,且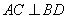 ,当四边形
,当四边形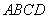 的面积S=
的面积S=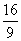 时,求直线L的方程.
时,求直线L的方程.
.【解析】(Ⅰ)设F(c,0),则直线L的方程为2x-y-2c=0,∵坐标原点O到L的距离为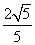 ,
,
∴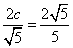 ,c=1。………………………………………………………2分
,c=1。………………………………………………………2分
∵椭圆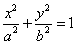 经过点
经过点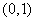 ,∴
,∴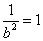 ,b=1,由
,b=1,由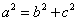 得
得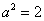 。
。
∴椭圆的方程为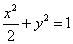 ……………………………………………4分
……………………………………………4分
(Ⅱ)由(Ⅰ)知,直线L过点F(1,0),设其方程为y=k(x-1)(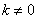 ),点A(
),点A(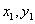 ),C(
),C(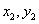 ),
),
解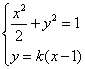 得,
得,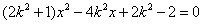 。
。
∴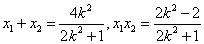 ,……………………………………………6分
,……………………………………………6分
 =
=
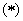 ………………………
……………………… ……
…… 8分
8分
∵过F的另一直线交椭圆于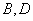 两点,且
两点,且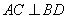 ,
, 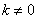 ,
,
∴直线BD的方程为y=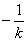 (x-1) 。
(x-1) 。
把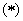 式中k换成
式中k换成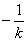 ,类比可得
,类比可得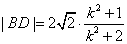 ,…………………………10分
,…………………………10分
∴四边形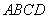 的面积
的面积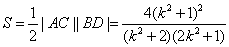
 , 解得
, 解得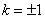 ,
,
∴直线L的方程为x-y-1=0或x+y-1=0 。 ………………………12分


 小夫子全能检测系列答案
小夫子全能检测系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com