
 已知在△ABC中,∠C=90°,∠BAC与∠ABC的角平分线交于点I,求证:AI•BI=$\sqrt{2}$AB•r(r为内切圆I的半径).
已知在△ABC中,∠C=90°,∠BAC与∠ABC的角平分线交于点I,求证:AI•BI=$\sqrt{2}$AB•r(r为内切圆I的半径). 分析 先证明∠AIB=180°-∠BAI+∠ABI=135°,再利用等面积,即可证明结论.
解答 证明:∵AI和BI分别为角平分线
∴∠BAI=$\frac{1}{2}$∠BAC,∠ABI=$\frac{1}{2}$∠ABC
∵∠C=90°,
∴∠BAC+∠ACB=90°
∴∠BAI+∠ABI=45°
∴∠AIB=180°-∠BAI+∠ABI=135°
∴S△ABI=$\frac{1}{2}$AI•BI•sin135°
∵S△ABI=$\frac{1}{2}$AB•r
∴AI•BI•sin135°=AB•r
∴AI•BI=$\sqrt{2}$AB•r(r为内切圆I的半径).
点评 本题考查三角形的内切圆,考查等式的证明,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
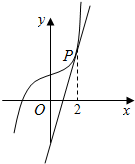 如图,已知函数f(x)=ax3+b,其图象上一点P处的切线为 l:y=4x-4,且点P的横坐标为2.
如图,已知函数f(x)=ax3+b,其图象上一点P处的切线为 l:y=4x-4,且点P的横坐标为2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4x}{(1-x)^{2}}$ | B. | -$\frac{4x}{(1-x)^{2}}$ | C. | $\frac{2}{(1-x)^{2}}$ | D. | -$\frac{2}{(1-x)^{2}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com