
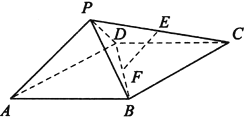
【题目】如图,四棱锥P—ABCD中,ABCD为矩形,△PAD为等腰直角三角形,
∠APD=90°,面PAD⊥面ABCD,且AB=1,AD=2,E、F分别为PC和BD的中点.
(1)证明:EF∥面PAD;
(2)证明:面PDC⊥面PAD;
(3)求四棱锥P—ABCD的体积.
【答案】(1)见解析(2)见解析(3)![]()
【解析】试题分析: (1)确定出EF∥AP,运用判断定理可证明.(2)抓住CD⊥AD,CD⊥面PAD,运用面面垂直的定理可证明.(3)确定PO为四棱锥P﹣ABCD的高.
求出PO=1,运用体积公式V=![]() PO×AB×AD求解即可.
PO×AB×AD求解即可.
试题解析:
(1)如图,连接AC,∵ABCD为矩形且F是BD的中点,∴AC必经过F,又E是PC的中点,所以,EF∥AP
∵EF在面PAD外,PA在面内,∴EF∥面PAD

(2)∵面PAD⊥面ABCD,CD⊥AD,面PAD![]() 面ABCD=AD,∴CD⊥面PAD,又AP
面ABCD=AD,∴CD⊥面PAD,又AP![]() 面PAD,∴AP⊥CD又∵AP⊥PD,PD和CD是相交直线且在面PDC内,∴AP⊥面PCD,又AD
面PAD,∴AP⊥CD又∵AP⊥PD,PD和CD是相交直线且在面PDC内,∴AP⊥面PCD,又AD![]() 面PAD,所以,面PDC⊥面PAD
面PAD,所以,面PDC⊥面PAD
(3)取AD中点为O,连接PO,因为面PAD⊥面ABCD及△PAD为等腰直角三角形,所以PO⊥面ABCD,即PO为四棱锥P—ABCD的高,∵AD=2,∴PO=1,
所以四棱锥P—ABCD的体积![]()


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:高中数学 来源: 题型:
【题目】已知产品![]() 的质量采用综合指标值
的质量采用综合指标值![]() 进行衡量,
进行衡量,![]() 为一等品;
为一等品;![]() 为二等品;
为二等品;![]() 为三等品.我市一家工厂准备购进新型设备以提高生产产品
为三等品.我市一家工厂准备购进新型设备以提高生产产品![]() 的效益,在某供应商提供的设备中任选一个试用,生产了一批产品并统计相关数据,得到频率分布直方图:
的效益,在某供应商提供的设备中任选一个试用,生产了一批产品并统计相关数据,得到频率分布直方图:
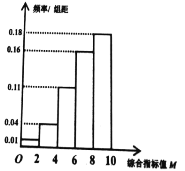
(1)估计该新型设备生产的产品![]() 为二等品的概率;
为二等品的概率;
(2)根据这家工厂的记录,产品各等次的销售率(某等次产品销量与其对应产量的比值)及单件售价情况如下:
一等品 | 二等品 | 三等品 | |
销售率 |
|
|
|
单件售价 |
|
|
|
根据以往的销售方案,未售出的产品统一按原售价的![]() 全部处理完.已知该工厂认购该新型设备的前提条件是,该新型设备生产的产品同时满足下列两个条件:
全部处理完.已知该工厂认购该新型设备的前提条件是,该新型设备生产的产品同时满足下列两个条件:
①综合指标值的平均数不小于![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
②单件平均利润值不低于![]() .
.
若该新型设备生产的产品![]() 的成本为
的成本为![]() 元/件,月产量为
元/件,月产量为![]() 件,在销售方案不变的情况下,根据以上图表数据,分析该新型设备是否达到该工厂的认购条件.
件,在销售方案不变的情况下,根据以上图表数据,分析该新型设备是否达到该工厂的认购条件.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() .
.
(1)求f(x)的极值;
(2)当0<x<e时,求证:f(e+x)>f(e﹣x);
(3)设函数f(x)图象与直线y=m的两交点分别为A(x1 , f(x1)、B(x2 , f(x2)),中点横坐标为x0 , 证明:f'(x0)<0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知关于x的二次函数f(x)=x2+(2t-1)x+1-2t.
(1)求证:对于任意t∈R,方程f(x)=1必有实数根;
(2)若![]() <t<
<t<![]() ,求证:方程f(x)=0在区间(-1,0)及
,求证:方程f(x)=0在区间(-1,0)及![]() 内各有一个实数根.
内各有一个实数根.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() sinωx+cosωx(ω>0)的图象与直线y=﹣2的两个相邻公共点之间的距离等于π,则f(x)的单调递减区间是( )
sinωx+cosωx(ω>0)的图象与直线y=﹣2的两个相邻公共点之间的距离等于π,则f(x)的单调递减区间是( )
A.[kπ+ ![]() ,kπ+
,kπ+ ![]() ],k∈z
],k∈z
B.[kπ﹣ ![]() ,kπ+
,kπ+ ![]() ],k∈z
],k∈z
C.[2kπ+ ![]() ,2kπ+
,2kπ+ ![]() ],k∈z
],k∈z
D.[2kπ﹣ ![]() ,2kπ+
,2kπ+ ![]() ],k∈z
],k∈z
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】秦九韶是我国南宋时代的数学家,其代表作《数书九章》是我国13世纪数学成就的代表之一,秦九韶利用其多项式算法,给出了求高次代数方程的完整算法,这一成就比西方同样的算法早五六百年,如图是该算法求函数f(x)=x3+x+1零点的程序框图,若输入x=﹣1,c=1,d=0.1,则输出的x的值为( )
A.﹣0.6
B.﹣0.69
C.﹣0.7
D.﹣0.71
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,点
,点![]() 与
与![]() 关于坐标原点对称,直线
关于坐标原点对称,直线![]() 垂直于
垂直于![]() 轴,垂足为
轴,垂足为![]() ,与抛物线交于不同的两点
,与抛物线交于不同的两点![]() ,
, ![]() ,且
,且![]() .
.
(1)求点![]() 的横坐标.
的横坐标.
(2)若以![]() ,
, ![]() 为焦点的椭圆
为焦点的椭圆![]() 过点
过点
(ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(ⅱ)过点![]() 作直线
作直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点,设
两点,设![]() ,若
,若![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,已知以M为圆心的圆M:x2+y2-12x-14y+60=0及其上一点A(2,4).
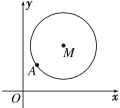
(1)设圆N与x轴相切,与圆M外切,且圆心N在直线x=6上,求圆N的标准方程;
(2)设平行于OA的直线l与圆M相交于B,C两点,且BC=OA,
求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知![]() :“直线
:“直线![]() 与圆
与圆![]() 相交”;
相交”; ![]() :“
:“![]() 有一正根和一负根”.若
有一正根和一负根”.若![]() 为真,
为真, ![]() 为真,求
为真,求![]() 的取值范围.
的取值范围.
(2)已知椭圆![]() :
: ![]() 与圆
与圆![]() :
: ![]() ,双曲线
,双曲线![]() 与椭圆
与椭圆![]() 有相同的焦点,它的两条渐近线恰好与圆
有相同的焦点,它的两条渐近线恰好与圆![]() 相切.求双曲线
相切.求双曲线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com